Co jsou lichá čísla a jak je poznat?

Než budeme hovořit o párných a lichých číslech, stojí za to objasnit několik bodů o tom, které skupiny čísel jsou obecně. To je nezbytné, aby se nepokusilo zjistit paritu zlomku.

Jaké jsou počty studií na základní škole?

První jsou přirozené. Také se poprvé objevily historicky. Lidstvo potřebovalo počítat položky. Navíc, když se nepočítá nula, tak to není zahrnuto do skupiny přirozených čísel. Zde jsou všechna celá čísla, která jsou větší než jedna.

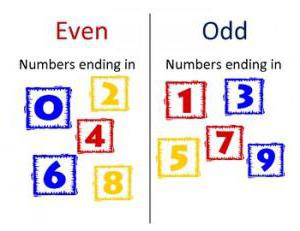
Pro ně je nejprve uvedena definice parity. Chcete-li pochopit, jaké číslo je liché, musíte si vzpomenout na znamení rovnoměrnosti. Skončí v jednom čísle: 0, 2, 4, 6, 8. Všechny ostatní budou zvláštní. Minimálně je jedna. Maximum neexistuje.

Jaké čísla se dělají?

Celé. Jejich soubor již obsahuje nulové a všechny záporné čísla. Řetězec přirozených čísel byl omezen vlevo a vpravo pokračoval neomezeně. S celými čísly se ukazuje nekonečný počet čísel a nalevo od nuly.

V tomto okamžiku se definice parity mírně změní. Nyní by mělo být děleno dvěma bez zbytku. Proto lichá čísla, dělená dvěma, dávají odpověď se zbytkem.

A dokonce je zadán i obecný záznam: pro sudý - 2n, lichý - (2n + 1). Pokud není pro přirozené maximum jen párné nebo liché, celá čísla nemají minimum.

A co co?

Rational (jiné jméno - skutečné) čísla. Kromě výše zmíněných obsahuje tato sada také zlomky. To znamená čísla, která mohou být reprezentována jako dvě. První z nich je čitatel a je reprezentován jako celé číslo. Druhým je jmenovatel, který není nikdy nulový.

Mimochodem, koncept parity není pro ně zaveden. Proto liché čísla psané jako zlomek vůbec neexistují.

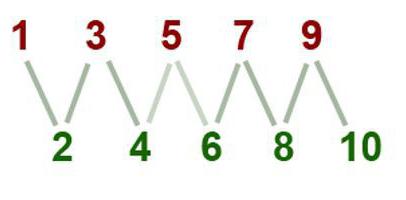
Jaké výsledky poskytují akce se sudými a lichými čísly?

Mohou být zváženy v pořadí zvětšující se složitosti aritmetické operace. Pak první a druhý budou doplněny a odečteny. Nezáleží na tom, který z nich je spuštěn, odpověď bude záviset pouze na počátečním páru čísel. Například pokud jsou počáteční čísla rovnoměrné, výsledek akce se rozdělí dvěma. Stejný výsledek bude, pokud je rozdíl nebo součet lichých čísel. Chcete-li získat liché číslo, musíte přidat nebo odečíst i liché číslo.

To lze snadno ověřit pomocí jejich obecného záznamu. Například přidání dvou sudých čísel: 2n + 2n = 4n = 2 * 2n. Zde 2n je sudé číslo, které je ještě násobeno dvěma. Takže to určitě bude zcela rozděleno do dvojice. To znamená, že odpověď je vyrovnaná.

Při přidávání i do lichého máme následující záznam: 2n + (2n + 1) = 4n + 1. První termín je sudé číslo, ke kterému je přidán jeden. Poslední termín nedovolí tento výsledek úplně rozdělit na dvě.

Třetí akcí je násobení. Když je proveden, bude vždy rovnoměrná odpověď, pokud existuje alespoň jeden rovnoměrný faktor. V situaci, kdy se dvě násobná čísla vynásobí, bude výsledek lichý.

Abyste je ilustrovali, je třeba provést následující zadání: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Opět první termín je sudé číslo a jednotka to bude divné.

Se čtvrtým dělením - divizí - vše není tak jasné. Můžete začít s dvěma vyrovnanými. Za prvé, zlomek se může ukázat, pak parita není otázka. Za druhé, výsledek je celé číslo. Ale ani tehdy nelze získat konečnou odpověď na otázku budoucí parity. Můžete ji vyhodnotit až po rozdělení. Odpověď může být jak lichá, tak lichá.

Pokud je liché číslo děleno sudým číslem, odpověď je vždy frakční. Proto jeho parita není určena.

Pokud se v divizi jedná o lichá čísla, výsledek může být také zlomek. Ale pokud je odpověď celá, pak bude určitě divné.

Při dělení i lichým, jako v předchozí situaci, existují dvě možnosti: zlomek nebo celé číslo. Ve druhém případě bude vždy vyrovnaný.