Jak vypočítat limity sekvencí?

Matematika je věda, která staví svět. Jako vědec a prostý člověk - nikdo nemůže bez něj dělat. Nejprve se malé děti naučí počítat, pak se přidávat, odečíst, množit a rozdělovat, na středních školách se objevují označení dopisů a ve starší, nemohou bez nich.

Ale dnes budeme mluvit o tom, na čem je vybudována všechna známá matematika. Na komunitě čísel s názvem "sekvenční limity".

Co jsou sekvence a kde je jejich limit?

Význam slova "sekvence" není těžké interpretovat. Jedná se o konstrukci věcí, kde je někdo nebo něco uspořádáno v určitém pořadí nebo ve frontě. Například fronta pro vstupenky do zoo - je posloupnost. A to může být jen jedno! Pokud se například podívejte na frontu v obchodě - jedná se o jednu sekvenci. A pokud jednou člověk náhle opustí tento řádek, pak je to další řádek, jiný příkaz.

Slovo "limit" je také snadno interpretováno - to je konec něčeho. Nicméně, v matematice, limity sekvencí jsou ty hodnoty na číselné čáře, ke kterým směřuje pořadí čísel. Proč se snaží a nekončí? Všechno je jednoduché, řada čísel nemá konec a většina sekvencí, jako jsou paprsky, má jen počátek a vypadá takto:

x ₁ , x ₂ , x ₃ , ... x _n ...

Proto definice sekvence je funkcí přirozeného argumentu. Jednoduše řečeno, jde o sérii členů nějaké sady.

Jak je postavena číselná sekvence?

Nejjednodušší příklad číselné sekvence může vypadat takto: 1, 2, 3, 4, ... n ...

Ve většině případů jsou z praktických důvodů sekvence vytvořeny z čísel a každý další člen série, označený jako X, má své vlastní jméno. Například:

x ₁ - první člen sekvence;

x ₂ - druhý člen sekvence;

x ₃ - třetí člen;

...

x _n je nth termín.

V praktických metodách je sekvence dána obecným vzorcem, ve kterém je nějaká proměnná. Například:

X _n = 3n, pak se řada čísel sama bude vypadat takto:

x ₁ = 3;

x ₂ = 6;

x ₃ = 9;

a tak dále

Neměli byste zapomenout, že ve všeobecném záznamu sekvencí můžete použít libovolné latinské písmeny, ne jen X. Například: y, z, k, atd.

Aritmetická progrese jako součást sekvencí

Než se podíváme na limity sekvencí, doporučujeme se ponořit hlouběji do samotného konceptu takové numerické série, kterou se všichni setkávali ve středních třídách. Aritmetická progrese je řada čísel, ve kterých je rozdíl mezi sousedními členy konstantní.

Úloha: "Let a ₁ = 15 a krok postupu číselné řady d = 4. Vybudovat první čtyři členy této série. "

Řešení: a ₁ = 15 (podle stavu) - první člen progrese (číselná řada).

a ₂ = 15 + 4 = 19 je druhým členem progrese.

a ₃ = 19 + 4 = 23 - třetí člen.

a ₄ = 23 + 4 = 27 je čtvrtým členem.

Tato metoda je však obtížně dosažitelná velkými hodnotami, např. ₁₂₅ .. Zvláště pro takové případy byl odvozen vzorec vhodný pro praxi: a _n = a ₁ + d (n - 1). V tomto případě ₁₂₅ = 15 + 4 (125-1) = 511.

Typy sekvencí

Většina sekvencí je nekonečná, stojí za to pamatovat na celý život. Existují dva zajímavé typy číselných řad. První je daná vzorem a _n = (- 1) ⁿ . Matematici často nazývají tuto sekvenci blikající. Proč Zkontrolujte jeho číselné řady.

-1, 1, -1, 1, -1, 1 atd. U takového příkladu je zřejmé, že čísla v sekvencích lze snadno opakovat.

Faktorní posloupnost. Je snadné odhadnout - faktoriál je přítomen ve vzorci, který definuje posloupnost. Například: a _n = (n + 1)!

Pak sekvence vypadá takto:

a ₁ = lx2 = 2;

a ₂ = lx2x3 = 6;

a ₃ = 1x2x3x4 = 24 atd.

Sekvence definovaná aritmetickou progresí se nazývá nekonečně klesající, pokud je nerovnost -1 pozorována u všech jejích členů. n = (-1/2) ⁿ .

a ₁ = - ½;

a ₂ = ¼;

a ₃ = - 1/8 atd.

Existuje dokonce sekvence tvořená stejným číslem. Takže a _n = 6 sestává z nekonečné množiny šest.

Určení limitu sekvence

Limity sekvencí již dlouho existují v matematice. Samozřejmě si zasloužili svůj vlastní kompetentní design. Takže čas naučit se definovat limity sekvencí. Nejprve zvažte podrobně limit pro lineární funkci:

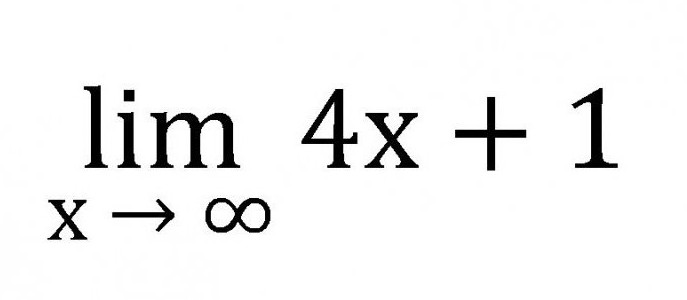
1. Všechny limity jsou zkráceny lim.
2. Limitový záznam se skládá ze zkratky lim, některé variabilní s ohledem na určité číslo, nulu nebo nekonečno a také z funkce samotné.

Je snadné pochopit, že definice limitu sekvence může být formulována následovně: je to určitý počet, ke kterému se všichni členové sekvence nekonečně přibližují. Jednoduchý příklad: a _x = 4x ​​+ 1. Pak sekvence sama vypadá takto.

5, 9, 13, 17, 21 ... x ...

Tato posloupnost se tedy nekonečně zvýší, a proto je její limit rovný nekonečnu jako x → ∞ a to by mělo být zapsáno následovně:

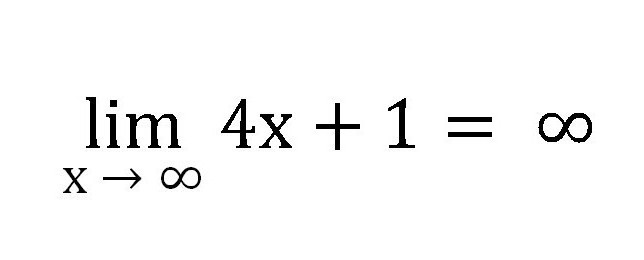
Pokud budeme mít podobnou sekvenci, ale x bude mít tendenci k 1, získáme:

a _x = 4x ​​+ 1.

Série čísel bude takto: 1,4, 1,8, 4,6, 4,944 a tak dále. Pokaždé, když potřebujete číslo stále více a více nahrazovat (0,1, 0,2, 0,9, 0,986). Z této série je zřejmé, že limit funkce je pět.

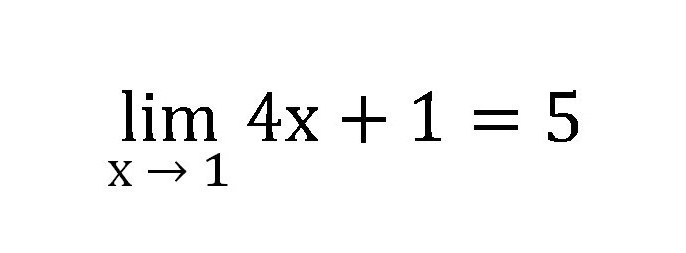
Z této části stojí za zmínku, jaký je limit číselné posloupnosti, definice a způsob řešení jednoduchých úkolů.

Obecné označení limitu sekvencí

Po prozkoumání limitu číselné sekvence, její definice a příkladů můžeme přistoupit k složitějšímu tématu. Absolutně všechny limity sekvencí mohou být formulovány s jedním vzorem, který je obvykle analyzován v prvním semestru.

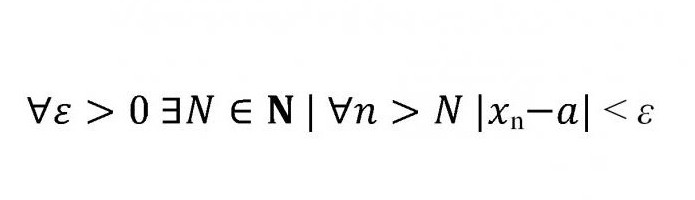
Co tedy znamená tato sada dopisů, modulů a nerovností?

∀ - kvantifikátor univerzálnosti, nahrazující fráze "pro všechny", "pro všechny" atd.

∃ - kvantifikátor existence, v tomto případě znamená, že existuje nějaká hodnota N patřící k množině přirozených čísel.

Dlouhá svislá tyčinka, po N, znamená, že daná sada N je "taková, že." V praxi to může znamenat "takové, že", "takové", atd.

Následuje modul. Je zřejmé, že modul je vzdálenost, která podle definice nemůže být záporná. Rozdílový modul je tedy přísně menší než "epsilon".

Chcete-li konsolidovat materiál, přečtěte si vzorec nahlas.

Nejistota a určitost limitu

Metoda pro nalezení limitu sekvencí, která byla diskutována výše, je jednoduchá při použití, ale v praxi to není tak racionální. Zkuste najít limit pro tuto funkci:

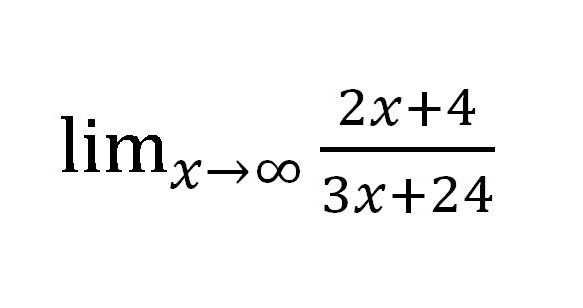
Pokud nahradíme různé hodnoty "X" (při každém zvýšení: 10, 100, 1000 atd.), Pak v čitateli dostaneme ∞, ale v jmenovateli také ∞. Ukazuje se to poněkud podivná frakce: 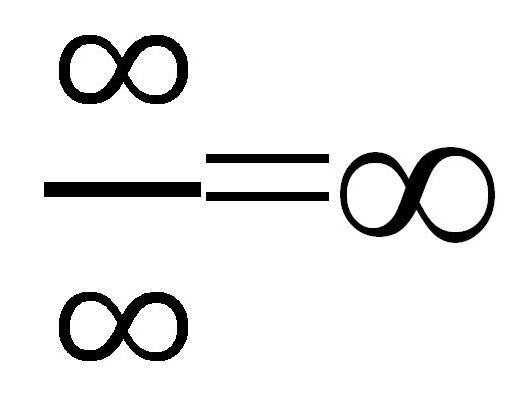Ale je to opravdu? Výpočet limitu číselné posloupnosti se v tomto případě zdá být poměrně snadný. Bylo by možné nechat všechno tak, jak je, protože odpověď je připravena a byla přijata za přiměřených podmínek, ale pro takové případy existuje ještě jiný způsob.

Nejprve najdeme nejvyšší výkon v čitateli zlomku - je to 1, protože x může být reprezentováno jako x ¹ .

Teď najdeme nejvyšší moc v jmenovateli. Také 1.

Rozdělíme čitateli i jmenovatele na proměnnou v nejvyšší míře. V tomto případě je frakce dělitelná x ¹ .

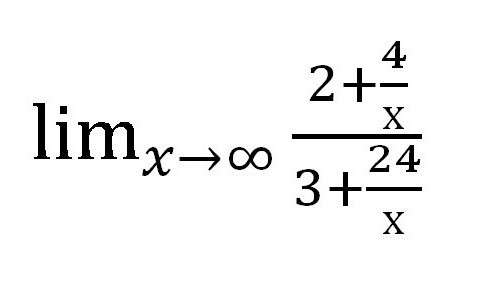
Dále zjistíme, jakou hodnotu má každá addenda obsahující proměnnou tendenci. V tomto případě je to zlomek. Jako x → ∞ hodnota každé frakce má tendenci nulovat. Při písemné práci stojí za to udělat poznámky pod čarou:

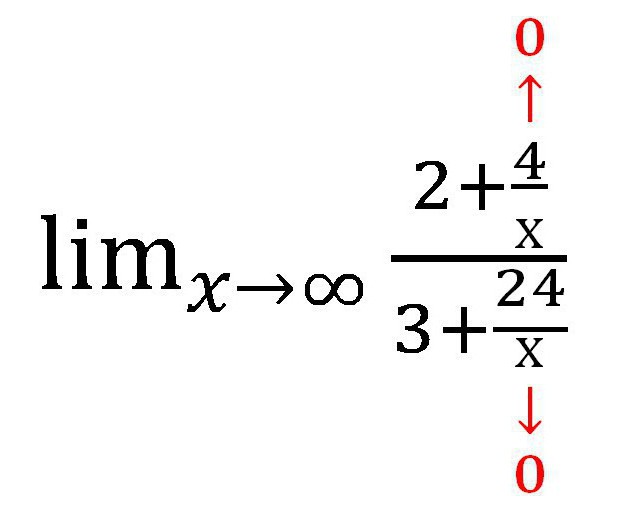
Získá se následující výraz:

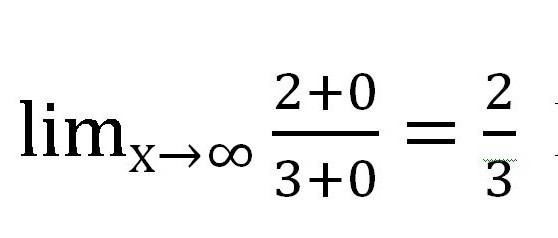
Samozřejmě, frakce obsahující x se nestaly nulami! Ale jejich hodnota je tak malá, že je úplně dovoleno, aby se při výpočtu nezohledňovala. Ve skutečnosti se x v tomto případě nikdy nebude rovnat 0, protože nula nemůže být rozdělena.

Co je okolí?

Předpokládejme, že profesor má k dispozici složitou posloupnost, danou samozřejmě ne méně složitou formulací. Profesor našel odpověď, ale je vhodný? Koneckonců, všichni lidé se mýlí.

Auguste Cauchy v jeho době přišel s velkým způsobem, jak dokázat limity sekvencí. Jeho metoda byla nazývána provozováním okolí.

Předpokládejme, že existuje nějaký bod a, jeho sousedství v obou směrech na číselné čáře je ε ("epsilon"). Vzhledem k tomu, že poslední proměnná je vzdálenost, je její hodnota vždy kladná.

Nyní definujeme nějakou posloupnost x _n a předpokládáme, že desátý termín sekvence (x ₁₀ ) vstoupí do sousedství a. Jak napsat tuto skutečnost v matematickém jazyce?

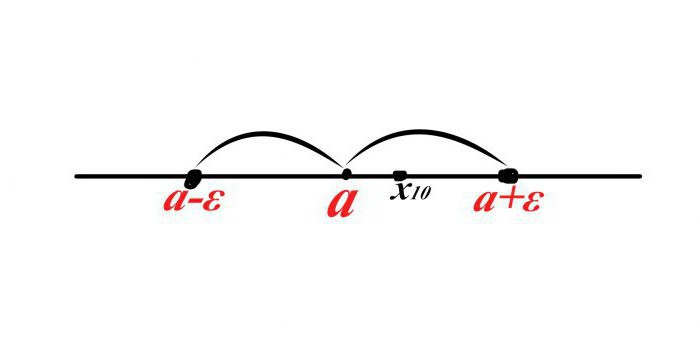
Předpokládejme, že x ₁₀ je vpravo od bodu a potom je vzdálenost x ₁₀ -a <ε, ale pokud umístíte "X desetinu" nalevo od bodu a, bude vzdálenost záporná, ale to není možné, pak byste měli do modulu přidat levou část nerovnosti. Dostáváme | x ₁₀ -a | <ε.

Nyní je čas objasnit v praxi tento vzorec, který byl zmíněn výše. Určité číslo a je správně nazýváno koncovým bodem sekvence, jestliže pro některý z jeho hranic je nerovnost ε> 0 splněna a celé okolí má své vlastní přirozené číslo N, takže všichni členové sekvence s významnějšími čísly budou uvnitř sekvence | x _n - a | <ε .

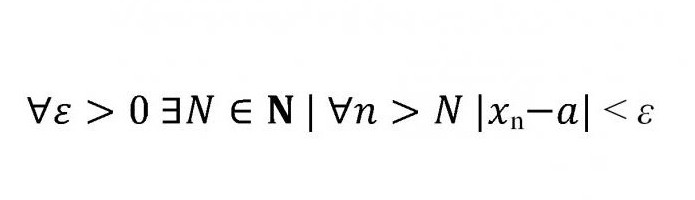
S takovými znalostmi je snadné implementovat řešení limitů sekvence, dokázat nebo vyvrátit připravenou odpověď.

Věty

Sezónní limitní věty jsou důležitou součástí teorie, bez níž je praxe nemožná. Existují pouze čtyři hlavní věty, které si pamatují, které je možné občas usnadnit průběh řešení nebo důkazu:

1. Jedinečnost limitu sekvence. Limit pro libovolnou sekvenci může být pouze jeden nebo vůbec ne. Stejný příklad s frontou, která může mít pouze jeden konec.
2. Pokud má řada čísel limit, pak je pořadí těchto čísel omezeno.
3. Limit součtu (rozdíl, produkt) sekvencí se rovná součtu (rozdíl, produkt) jejich limitů.
4. Limit kvocientu z dělení dvou sekvencí je stejný jako kvocient mezních hodnot, pokud a pouze pokud jmenovatel nezmizí.

Důkaz sekvencí

Někdy je nutné vyřešit inverzní problém, dokázat daný limit číselné posloupnosti. Zvažte příklad.

Dokažte, že limit sekvence daný vzorem je nulový.

Podle pravidla popsaného výše musí být pro jakoukoliv sekvenci splněna nerovnost | x _n - a | <ε. Nahraďte zadanou hodnotu a referenční bod. Máme:

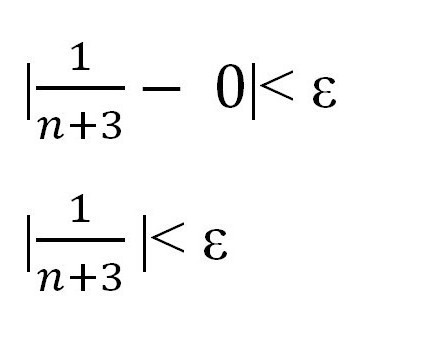
Express n přes "epsilon" ukázat existenci určitého čísla a prokázat existenci limitní sekvence.

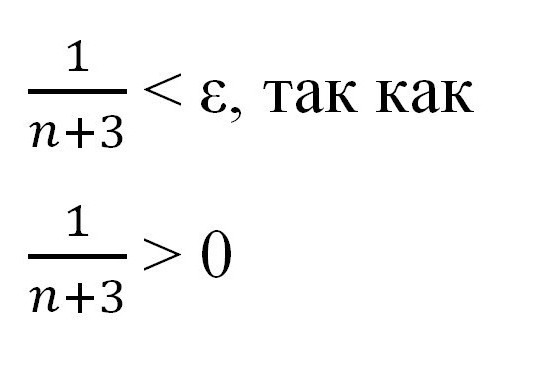
V této fázi je důležité připomenout, že "epsilon" a "en" jsou kladná a nenulová čísla. Nyní můžete pokračovat v dalších transformacích pomocí znalostí nerovností získaných na střední škole.

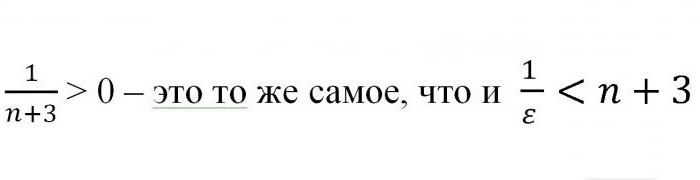
Odkud se ukázalo, že n> -3 + 1 / ε. Vzhledem k tomu, že stojí za zmínku, že mluvíme o přirozených číslech, lze výsledek zaokrouhlit vložením do hranatých závorek. Bylo tedy prokázáno, že pro jakoukoli hodnotu sousedství "epsilon" bodu a = 0 byla hodnota taková, že počáteční nerovnost platí. Z tohoto můžeme bezpečně říci, že číslo a je limit dané sekvence. Co bylo nutné prokázat.

S takovou pohodlnou metodou lze dokázat hranici číselné sekvence, ať už se to na první pohled může zdát složité. Hlavní věc - neměňte paniku při pohledu na práci.

Nebo možná ne?

Existence limitní sekvence je v praxi volitelná. Můžete snadno najít takovou řadu čísel, která skutečně nemají žádný konec. Například stejný blikač x _n = (-1) ⁿ . je zřejmé, že sekvence sestávající pouze ze dvou čísel, cyklicky se opakující, nemůže mít limit.

Stejná historie se opakuje se sekvencemi sestávajícími z jednoho čísla, částečné, které má v průběhu výpočtu nejistotu libovolného pořadí (0/0, ∞ / ∞, ∞ / 0 atd.). Mělo by se však pamatovat na to, že se také provádí nesprávný výpočet. Někdy limity sekvencí pomohou znovu prověřit vlastní řešení.

Monotónní sekvence

Dále jsme uvažovali o několika příkladech sekvencí, metodách jejich řešení a nyní se pokusíme přijmout konkrétnější případ a nazvat ho "monotonní sekvencí".

Definice: je spravedlivé volat jakoukoli sekvenci monotonně se zvyšující, pokud pro ni drží přísnou nerovnost x _n <x _{n +1.} Také jakákoli sekvence je správně nazývána monotónním snižováním, jestliže pro ni zůstává nerovnost x _n > x _{n +1.}

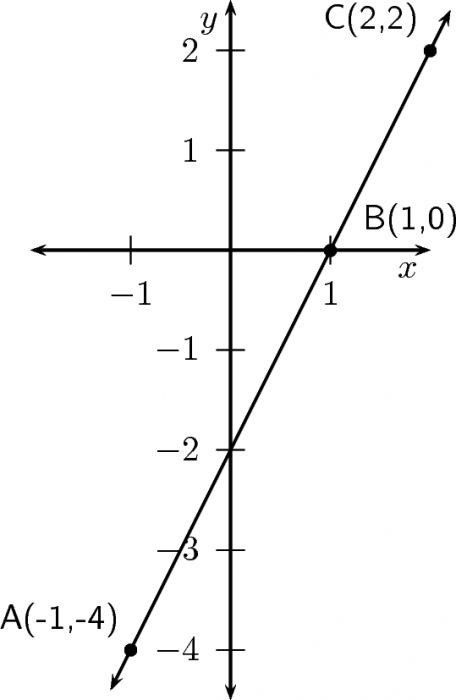
Spolu s těmito dvěma podmínkami existují podobné slabé nerovnosti. Proto x _n ≤ x _{n +1} (neklesající posloupnost) a x _n ≥ x _{n +1} (nekončící sekvence).

Ale je to jednodušší pochopit pomocí příkladů.

Sekvence daná vzorcem x _n = 2 + n vytváří následující řadu čísel: 4, 5, 6 atd. Jedná se o monotonicky rostoucí posloupnost.

A pokud vezmeme x _n = 1 / n, dostaneme sérii: 1/3, ¼, 1/5 atd. Jedná se o monotonicky klesající posloupnost.

Limit konvergentní a omezené posloupnosti

Ohraničená sekvence - sekvence, která má limit. Sbližující se sekvence je řada čísel, která má nekonečně malý limit.

Tudíž hranice ohraničené sekvence je jakákoli platná nebo komplexní číslo. Nezapomeňte, že může existovat pouze jeden limit.

Limit konvergující sekvence je nepatrné množství (skutečné nebo složité). Pokud nakreslíte schéma sekvence, pak se v určitém bodě bude shodovat, snažit se obrátit na určitou hodnotu. Proto jména - konvergentní sekvence.

Monotónní limit

Limit pro takovou sekvenci může nebo nemusí být. Zpočátku je užitečné pochopit, kdy to je, z čehož se člověk může odrazit, když prokáže nepřítomnost limitu.

Mezi monotónními sekvencemi se vyskytují konvergující a divergentní. Konverze je sekvence, která je tvořena množinou x a má v sadě skutečný nebo složitý limit. Rozdílná - sekvence, která nemá v sérii žádné omezení (ani reálné, ani složité).

Sekvence se navíc sbíhá, pokud její geometrický obraz sbližuje horní a spodní hranice.

Limit konvergující sekvence může být v mnoha případech rovný nule, protože každá nekonečně malá sekvence má známý limit (nula).

Nezáleží na tom, jakou sblíženou sekvenci jsou všechny omezené, ale ne všechny ohraničené sekvence konvergují.

Součet, rozdíl, produkt dvou konvergujících sekvencí je také konvergentní sekvencí. Kvocient však může být konvergentní, pokud je definován!

Různé akce s omezeními

Limity sekvencí jsou ve většině případů stejně velké jako čísla a čísla: 1, 2, 15, 24, 362 atd. Ukázalo se, že některé operace mohou být provedeny s omezeními.

Za prvé, jako čísla a čísla, mohou být přidány a odečteny limity libovolných sekvencí. Na základě třetí věty o limitech sekvencí platí následující rovnost: hranice součtu sekvencí se rovná součtu jejich limitů.

Za druhé, na základě čtvrté věty o limitech sekvencí platí následující rovnost: hranice produkce ného počtu sekvencí je rovna výsledku jejich limitů. Totéž platí pro dělení: hranice kvocientu dvou sekvencí se rovná kvocientu jejich limitů za předpokladu, že mez není nula. Koneckonců, pokud se limit sekvencí rovná nule, dostaneme to rozdělení podle nuly, což je nemožné.

Vlastnosti sekvence

Zdá se, že hranice numerické posloupnosti již byla podrobně analyzována, ale takové výrazy jako "nekonečně malé" a "nekonečně velká" čísla jsou zmíněny více než jednou. Je zřejmé, že pokud existuje sekvence 1 / x, kde x → ∞, pak je taková zlomek nekonečně malá a pokud je sekvence stejná, ale limit má tendenci k nule (x → 0), pak se frakce stává nekonečně velkým množstvím. A tato množství mají své vlastní vlastnosti. Vlastnosti limitu sekvence mající jakékoliv malé nebo velké hodnoty jsou následující:

1. Součet libovolného množství libovolně malých množství bude také malým množstvím.
2. Součet jakéhokoli množství velkých množství bude nekonečně velké množství.
3. Produkt libovolně malých množství je nekonečně malý.
4. Produkt libovolného počtu velkých čísel je nekonečně velká hodnota.
5. Pokud původní sekvence inklinuje k nekonečně velkému číslu, potom bude protilehlé množství nekonečně malé a bude mít tendenci k nule.

Ve skutečnosti výpočet limitu sekvence není tak obtížným úkolem, pokud znáte jednoduchý algoritmus. Ale limity sekvencí - téma, které vyžaduje maximální pozornost a vytrvalost. Samozřejmě, stačí jen chytit podstatu řešení těchto výrazů. Počínaje malými, v průběhu času se můžete dostat do velkých vrcholků.