Jak najít hypotenzu: 4 způsoby, jak najít odpověď

Po studiu tohoto tématu pravé trojúhelníky studenti často odmítají všechny informace o nich. Včetně toho, jak najít hypotenzu, nemluvě o tom, co to je.

A marně. Protože později se diagonál obdélníku ukáže jako velmi hypotenuse a je třeba ji najít. Or průměr kruhu se shoduje s největší stranou trojúhelníku, jehož rohy jsou rovné. A najít to bez těchto poznatků je nemožné.

Existuje několik možností pro nalezení hypotenze trojúhelníku. Volba metody závisí na počáteční množině dat ve výpisu hodnot problémů.

Metoda číslo 1: obě jsou uvedeny

Toto je nejpamátnější metoda, protože používá pythagorskou větu. Pouze někdy studenti zapomínají, že tento vzorec je čtvercem hypotenze. Takže abyste našli stranu samotnou, musíte ji extrahovat druhá odmocnina. Proto vzorec pro hypotenzu, který je obvykle označen písmenem "c", bude vypadat takto:

c = √ (a ² + ² ) , kde jsou ^dvě písmena pravého trojúhelníku napsána písmeny "a" a "b".

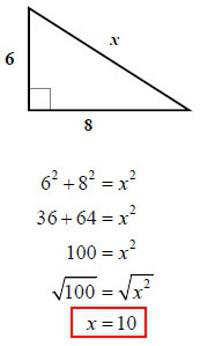
Metoda č. 2: Známá noze a úhlu, který je vedle ní

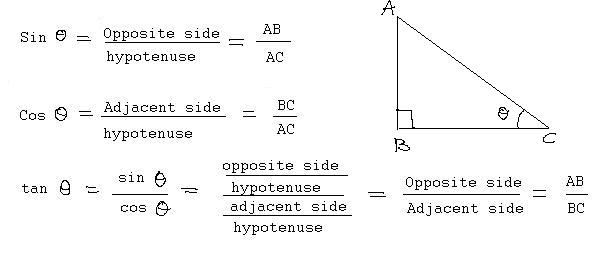
Chcete-li zjistit, jak najít hypotenzu, budete muset vyvolat trigonometrické funkce. Konkrétně kosinus. Pro pohodlí předpokládáme, že je uvedena noha "a" a úhel α sousedící s ní.

Nyní si musíme pamatovat, že kosinus úhlu pravoúhlého trojúhelníku se rovná poměru obou stran. Čitatel bude hodnota nohy a jmenovatel - hypotenuse. Z toho vyplývá, že druhá může být počítána podle vzorce:

c = a / cos α .

Metoda číslo 3: vzhledem k noze a úhlu, který stojí proti němu

Abychom se nezachytili ve vzorcích, uvedeme notaci pro tento úhel - β, a necháme stranu starého "a". V tomto případě je nutná další funkce trigonometru, sinus.

Stejně jako v předchozím příkladu je sinus rovný poměru nohy k hypotenze. Vzorec této metody je následující:

c = a / sin β .

Abyste se nezapadli do trigonometrických funkcí, můžete si zapamatovat jednoduché mnemotechnické pravidlo: pokud se problém týká protilehlého úhlu, pak musíte použít s a nus, pokud jde o pr a ležení, pak k sine. Pozornost by měla být věnována prvním samohláskům v klíčových slovech. Vytvářejí dvojice o-a nebo -o .

Metoda číslo 4: podél obvodu obvodového pláště

Nyní, abychom se naučili, jak najít hypotenzu, musíme připomenout vlastnost kruhu, který je popsán kolem pravého trojúhelníku. To zní takto: Střed kruhu se shoduje se středem hypotenze. Jinak řečeno, největší stranou pravého trojúhelníku je diagonální kružnice. To znamená, zdvojnásobte poloměr. Vzorec pro tento úkol bude vypadat takto:

c = 2 * r , kde r je známý poloměr.

To jsou všechny možné způsoby nalezení hypotenze pravého trojúhelníku. Chcete-li použít v každém konkrétním úkolu, potřebujete metodu, která je vhodnější pro sadu dat.

Příklad číslo problému 1

Stav: v pravém trojúhelníku jsou mediány přitahovány k oběma nohám. Délka, kterou držel na větší straně, je √52. Druhý medián je dlouhý √73. Vyžadováno pro výpočet hypotenze.

Rozhodnutí.

Vzhledem k tomu, že mediány jsou nakresleny v trojúhelníku, rozdělují nohy na dva stejné segmenty. Pro usnadnění, odůvodnění a zjištění, jak najít hypotenzu, musíte zadat několik symbolů. Nechť obě poloviny většího katehetu budou označeny písmenem "x" a druhým písmenem "y".

Teď musíme zvážit dva pravé trojúhelníky, jejichž hypoteny jsou známé mediány. Pro ně je třeba napsat dvakrát Pythagoreanova věta :

(2y) ² + x ² = (√52) ²

a

(y) ² + (2x) ² = (√73) ² .

Tyto dvě rovnice tvoří systém se dvěma neznámymi. Po jejich vyřešení bude snadné najít nohy původního trojúhelníku a podle nich jeho hypotenzu.

Nejprve musíte stavět vše do druhého stupně. Ukazuje se:

4y ² + x ² = 52

a

při ² + 4x ² = 73.

Z druhé rovnice lze vidět, že ² = 73 - 4x ² . Tento výraz musí být nahrazen prvním a vypočítat "x":

4 (73 - 4 x ² ) + x ² = 52.

Po konverzi:

292 - 16 x ² x ² = 52 nebo 15 x ² = 240.

Z posledního výrazu x = √16 = 4.

Nyní můžete vypočítat "y":

y ² = 73 - 4 (4) ² = 73 - 64 = 9.

y = 3.

Podle podmínky se ukazuje, že nohy původního trojúhelníku jsou 6 a 8. Proto můžete použít vzorec z první metody a najít hypotenzu:

√ (6 ² + 8 ² ) = √ (36 + 64) = √100 = 10.

Odpověď : hypotenze je 10.

Příklad úkolového čísla 2

Stav: vypočítá se diagonál nakreslený v obdélníku s menší stranou rovnající se 41. Je-li známo, že rozděluje úhel o ty, které se vztahují jako 2 na 1.

Rozhodnutí.

V tomto úkolu je úhlopříčka obdélníku největší stranou v trojúhelníku s úhlem 90 °. Proto se všechno shoduje na tom, jak najít hypotenzu.

Problém je kolem rohů. To znamená, že budete muset použít jednu z vzorců, ve kterých existují trigonometrické funkce. Nejprve musíte určit hodnotu jednoho z ostrých rohů.

Nechť menší z úhlů uvedených ve stavu je α. Pak bude pravý úhel, který je dělený diagonálem, rovný 3α. Matematická notace pro toto je:

90 ° = 3 α.

Z této rovnice jednoduše určíme α. To bude rovno 30 °. A bude ležet naproti menší straně obdélníku. Proto budete potřebovat vzorec popsaný v metodě číslo 3.

Hypotenuse se rovná poměru nohy k sinusu protilehlého úhlu, to znamená:

41 / sin 30 ° = 41 / (0,5) = 82.

Odpověď: hypotenze je 82.