Tsiolkovský vzorec: použití a příklad
Vzorec Konstantina Eduardova Tsiolkovského vyjadřuje maximální rychlost letadla, které dosáhne během letu tryskem. Získává se integrací Meshcherskyho rovnice.
Formula Tsiolkovsky
Tento vzorec vyjadřuje rychlost rakety přenášené plyny z hořeného paliva. Meshcherskyova rovnice a Tsiolkovský vzorec jsou neoddělitelně propojeny - Mechcherskyova rovnice popisuje hmotu hmotného bodu, který se mění s časem, zatímco proud tryskové rakety neustále snižuje svou hmotnost v důsledku spalování paliva. Změna rychlosti s měnící se hmotností (v našem případě se snižuje) pohybujícího se těla - to je to, co říká proudový pohon. Tsiolkovského vzorec je založen na tom.
Pro řešení řady problémů teoretické mechaniky v oblasti proudového pohonu je použita Mechcherskyova rovnice (základní rovnice hmotného bodu proměnné hmotnosti) a Tsiolkovského vzorce (vzorec poslední rychlosti letadla), které se nazývají základní vztahy teorie proudového pohonu.
Základem pro návrh a plánování v oblasti vesmírného letu je přesně Tsiolkovský vzorec, jehož závěr byl skutečný průlom pro průzkum vesmíru.
Úkoly Tsiolkovského
Aby vyřešil problém meziplanetárních letů, K.E. Tsiolkovský považoval raketu za prostředek letu. Odvodil vzorec, který lze použít k určení závislosti hmotnosti letadla na palivu a míry oddělení spalovacích produktů rakety používané palivo vzhledem k ní. Ukazujeme dva jeho úkoly:
- Studium pohybu tělesa s proměnnou hmotností s jedinou reaktivní silou působící na něj.
- Studium pohybu těla v jednotném těžišti proměnné hmotnosti blízko povrchu Země
Předmluva
Pro všechny kosmické lety byl výchozím a základním vzorem Tsiolkovského pro rychlost rakety, jehož výstup je uveden níže.
Nejprve je třeba, abyste zhruba mluvili o podstatném bodě. Síly gravitace Země a jiných nebeských těl budou působit na ni (v okamžiku vzletu bude samozřejmě gravitační síla Země nejsilnější), síla odporu vzduchu na jedné straně a protilehlá směrová reaktivní síla vyplývající z uvolnění spáleného plynu v základně . Raketa s velkou silou vysílá tyto plyny, které jí říkají, že zrychlení směřuje naproti straně emisí. Nyní musíte tyto argumenty předložit ve formě vzorce.
Princip samotného raketového letu je poměrně jednoduchý. Při vysoké rychlosti uniká z rakety plyn, který vzniká spalováním paliva, který dává raketě určitou sílu, která působí proti směru pohybu. Vzhledem k tomu, že se předpokládá, že na raketě nepůsobí vnější síly, systém bude uzavřen a jeho hybnost nezávisí na čase.
Meshchersky rovnice
Jedním z hlavních příkladů pohybu tělesa s měnící se hmotou je raketa s jedinou etapou, jejíž hmota se mění pouze v důsledku spalování jím poháněného paliva. Hmotnost takové rakety se skládá z nezměněné (vlastní raketa a užitečné zatížení) a variabilní (palivo). Takovým příkladem je zjednodušený model.
V moderní raketové výrobě se však používají vícestupňové rakety. Principy jejich práce spočívají v tom, že vzhledem k velkému objemu schodů jsou schopni po vzletu dopravovat a používat mnohem více paliva. Po spalování je raketa hlášena významným impulsem (mnohem větší než to, co lze dosáhnout pomocí jednoho stupně), a části, které se zbytečně oddělují od základny, snižují celkovou hmotnost o 80-90%. Pro výpočet parametrů vícestupňové rakety je však nutné doplnit ukazatele jednotlivých komponent.
Diferenciální rovnice Meshchersky popisuje pohyb materiální bod s proměnnou hmotností.
(m + dm) (υ + dy) + dm 'υ' - mύ = Fdt - v čase dt (rozdíl mezi sílou v čase t a dt + t bude přírůstek).
Kde m a υ závisí na čase, dt - nějaký čas letu. Pro to je tvořena síla pohybu plynu - dm 'υ', dm '- hmotnost plynu vytvořeného z paliva. F je výsledná síla.
Ve výše uvedeném vyjádření se přírůstek hmotnosti rakety, plynu a rychlosti pohybuje na nulu, takže výraz má následující podobu:
mdy = υ''dm + Fdt,
navíc, υ "se rovná rozdílu mezi rychlostí plynu a rychlostí plynu a je rychlost odtoku plynu.
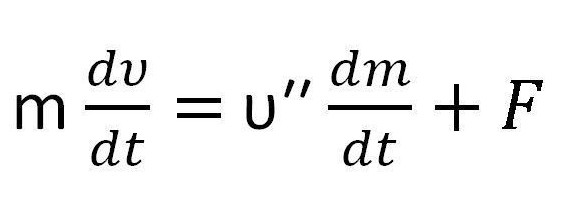 - rovnice ve formě se začíná shodovat s druhým zákonem Newtona - F = ma = m
- rovnice ve formě se začíná shodovat s druhým zákonem Newtona - F = ma = m
Nazývá se Meshcherskyho rovnice.
Odvození vzorce Tsiolkovsky
Je nutné odvodit vzorec popisující pohyb tělesa s proměnnou hmotností. Formula Tsiolkovskij je takový. Výstup je uveden níže.
Při těchto výpočtech se předpokládá, že vnější síly nepůsobí na pohybujícím se těle, tj. F = 0.
Pak mdυ = υ''dm
Vzhledem k tomu, že dopad vnějších sil na letící rakety je nulový, pohybuje se v přímce a rychlost pohybu je protilehle rychlosti plynu. V souladu s tím, υ = -y "
Ukazuje se, že musí být integrován.
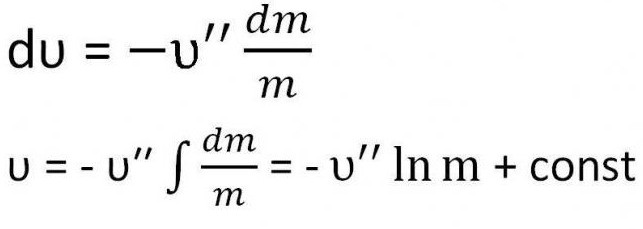
Je třeba najít konstantu. Za tímto účelem stačí nahradit počáteční podmínky rovnicí - rychlost je nula a hmotnost - součet hmotnosti paliva a hmoty rakety
Obecně řečeno, m ve vzorci se skládá ze dvou parametrů - od užitečného zatížení a konstrukce rakety. Užitným nákladem je celková hmotnost nákladu a posádky.
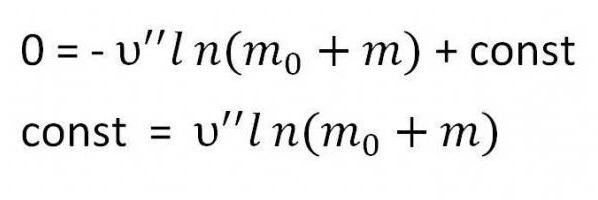
Ve vzorci nahrazujeme nalezenou konstantu. V důsledku toho se získá požadovaná formulace.
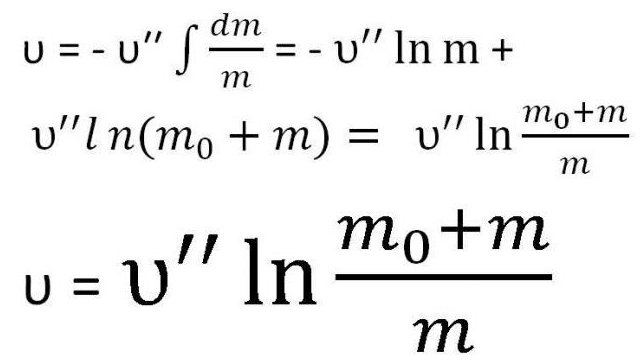
To je jedna z variant Tsiolkovského vzorce pro rychlost. Někdy je však nutno brát v úvahu právě hmotu. Proto je někdy napsáno následovně:
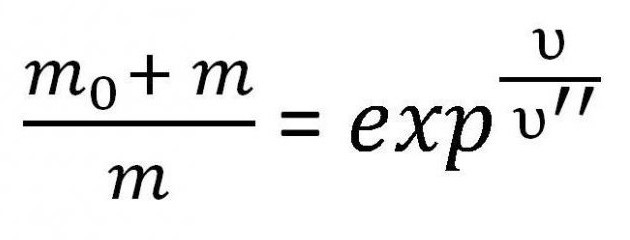
Tento vzorec se používá k výpočtu hmotnosti paliva, která je potřebná pro vývoj určité rychlosti za stanovených podmínek.
Budu dále zvažovat malý úkol. Předpokládejme, že raketa potřebuje vyvinout první kosmickou rychlost pro rotaci podél oběžné dráhy Země. Potřebujete to nejprve vypočítat hmotnost palivo, samozřejmě. Pak je velmi jednoduché to vyjádřit z Tsiolkovského vzorce.
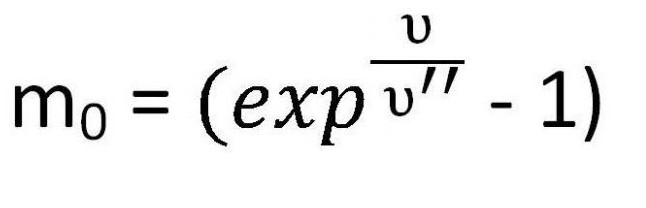
Relativistická mechanika
Všechny výše uvedené vzorce lze použít pouze v případě, kdy je rychlost rakety mnohem nižší než rychlost světla (υ < Pokud však rychlost rakety může být porovnána s rychlostí světla, je nutné použít i jiné zákony. Nechť m a υ je hmotnost rakety ve stavu a její rychlost kdykoliv v čase t, a υ 'a m' je rychlost uvolňování plynu a její hmotnost současně. To znamená, že m 'je hmotnost uvolněného plynu, takže jeho hodnota pro výpočet je nevýznamná, m' = 0. Je zapotřebí napsat zákon zachování hybnosti a práva zachování energie v relativistické mechaniky, potom rozlišujeme první rovnici, vzhledem k tomu, že m '= 0 a získáme třetí výraz. kde u je rychlost emise plynů. Na základě zákona o přidání rychlosti v relativistické mechaniky následuje tento výraz. Musí být převedena s ohledem na υ 'a integrována pro získání konečné verze rovnice. Pak získáme Tsiolkovského vzorce pro rychlost, srovnatelnou s rychlostí světla. Může se také nazývat relativistickým vzorem Tsiolkovského. Tento úkol můžete poněkud komplikovat a považovat za příklad raketu s několika etapami. Tsiolkovský vzorec pro vícestupňovou raketu je součtem parametrů nezbytných pro výpočet. To znamená, že pro výpočet rychlosti pro vícestupňovou raketu byste měli zvýšit rychlost každé součásti. Základem všech vesmírných letů je Tsiolkovský vzorec. Při výpočtu letu je důležité jasně pochopit, jaké procento energie získané po spalování paliva se používá jako užitečná práce? Účinnost se tudíž označuje jako poměr kinetické energie rakety a plyny po vysunutí. Označte m a m 'za hmotnost rakety na začátku a na konci letu, kontinuální čas t. Podle toho - rychlost vypuzování plynů. Poté, podle vzorce Tsiolkovského, účinnost raketového motoru lze nalézt takto: Je třeba poznamenat, že tato účinnost je velmi malá a nepřesahuje 5%, navíc, stejně jako u tepelných motorů, tento ukazatel se rovná 80%. Některé zdroje používají mírně odlišný vzorec Tsiolkovského, což je rovnice, ve které je namísto υ '-I použit jiný parametr. . První otázkou, která přichází na mysli, je otázka dimenzionality. Na rozdíl od rychlosti má hybnost jiný rozměr, který bude v rozporu s podstatou vzorce. Samotný impuls se však shoduje v rozměru s rychlostí. Zvláštní impuls udává počet sekund, ve kterých motor po zaplnění jednotky paliva přijme jednotku síly. Používá se výlučně v popisu tryskového motoru. Tsiolkovského vzorec pro vícestupňovou raketu se používá také při konstrukci rakety. Za tímto účelem se používá zcela logický vztah, který je prakticky přímo proporcionální - čím více paliva se používá při létání, tím větší bude hmotnost samotné rakety. To je způsobeno skutečností, že pro přepravu velkého množství paliva jsou požadovány velké nádrže, takže velikost lodi a dokonce i samotný motor vzrůstá. Některým řešením problému je použití tuhých paliv, které vyžadují menší skladovací podmínky. V současné době však má nejmenší specifický impuls stávajících. Tsiolkovský vzorec je také používán k výpočtu potřebného množství paliva pro vývoj určité rychlosti - obvykle jeden ze čtyř kosmických. 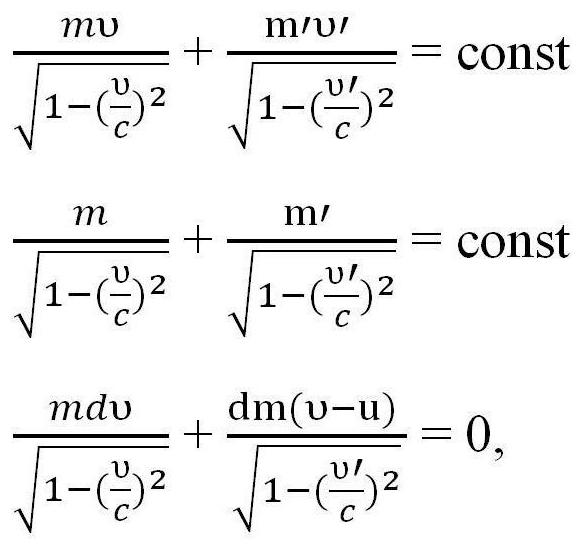
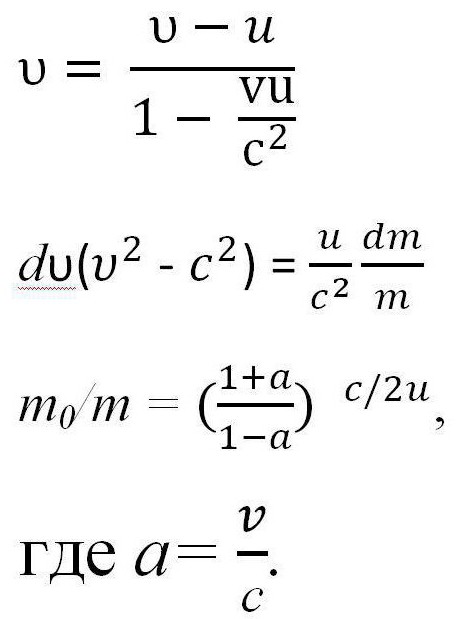
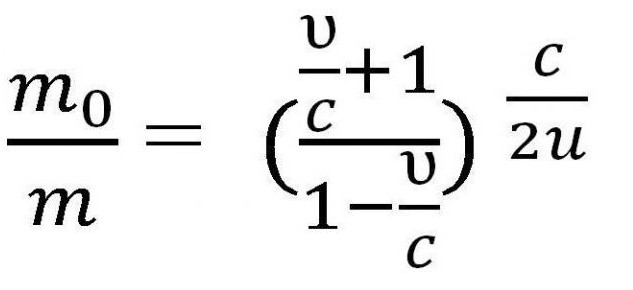
Několik závěrů z vzorce Tsiolkovsky
Účinnost rakety
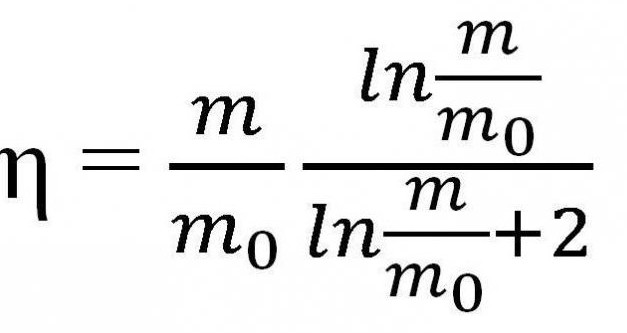
Další forma vzorce
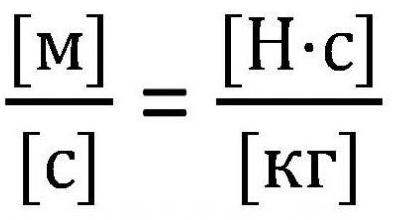
Použijte při vytváření střel
Rychlost místa