Co je integrál? Integrály s detailním řešením. Integrovaná tabulka
Slovo "integrál" pochází z latinského integrálu - holistického. Tento titul je navržen v 17. století. student vynikajícího Leibnizu (a také vynikajícího matematika) I. Bernoulliho. A jaký je integrál v moderním smyslu? Níže se budeme snažit poskytnout komplexní odpověď na tuto otázku.
Historické pozadí konceptu integrálu
Na počátku 17. století v úvahu vedoucích vědců bylo velké množství fyzických (především mechanických) úkolů, při nichž bylo nutné zkoumat závislost některých veličin na ostatních. Nejvíce zřejmými a naléhavými problémy bylo zjištění okamžité rychlosti nerovnoměrného pohybu těla v daném okamžiku a jeho nepřímé problémy se zjištěním velikosti cesty, jíž tělo cestuje po určitou dobu během tohoto pohybu. Dnes už víme, jaký je integrál rychlosti pohybu - je to cestovní cesta. Ale pochopení, jak jej vypočítat, znát rychlost v každém okamžiku, se nezjistilo okamžitě.
Nejprve z úvahy o takových závislostech fyzikálních veličin, například cesty o rychlosti, se vytvořil matematický pojem funkce y = f (x). Studium vlastností různých funkcí vedlo k vzniku matematická analýza. Vědci aktivně hledají způsoby studia vlastností různých funkcí. 
Jak byl výpočet integrálů a derivátů?
Poté, co Descartes vytvořil základy analytické geometrie a příležitost graficky znázornit funkční závislost v osách karteziánského souřadného systému, vědci čelili dvěma hlavním novým úkolům: jak nakreslit tečnu na zakřivenou čáru v jakémkoliv bodě a jak najít plochu postavy ohraničené nad touto křivkou a přímky, rovnoběžně s osami souřadnic. Neočekávaným způsobem se ukázalo, že první je ekvivalentní zjištění okamžité rychlosti a druhá zjištění ujeté vzdálenosti. Koneckonců v případě nerovnoměrného pohybu byla zobrazena v kartézských osách souřadnic "vzdálenost" a "čas" s určitou zakřivenou čárou.
Genius Leibniz a Newton v polovině 17. století. byly vytvořeny metody, které umožnily vyřešit oba problémy. Ukázalo se, že pro provedení dotyku na křivku v určitém bodě je nutné nalézt hodnotu takzvaného derivátu funkce popisující tuto křivku v daném bodě a tato hodnota se rovná rychlosti změny funkce, tj. S odkazem na závislost "cesta versus rychlost" okamžitá rychlost těla.
Abychom našli oblast ohraničenou křivkou, bylo nutné vypočítat určitý integrál, který dává přesnou hodnotu. Derivace a integrál - základní pojmy diferenciálního a integrálního počtu, které jsou základem moderní matematické analýzy - nejdůležitější sekce vyšší matematiky.
Plocha pod křivkou
Tak jak ji definovat přesná hodnota? Pokusme se od samého začátku podrobně odhalit proces výpočtu prostřednictvím integrálu.
Nech f je spojitá funkce v intervalu [ab]. Zvažte křivku y = f (x) na obrázku níže. Jak najít oblast oblasti ohraničenou křivkou), osou x a řádky x = a a x = b? To znamená, že oblast stínovaného obrázku na obrázku. 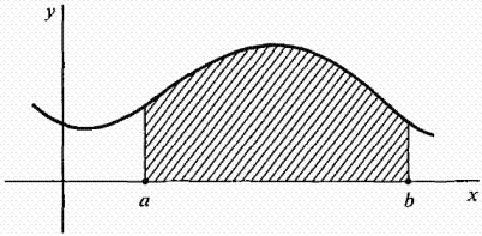
Nejjednodušší případ je, když f je konstantní funkce; to znamená, že křivka je vodorovná čára f (X) = k, kde k je konstanta a k ≥ 0, jak je znázorněno na obrázku níže. 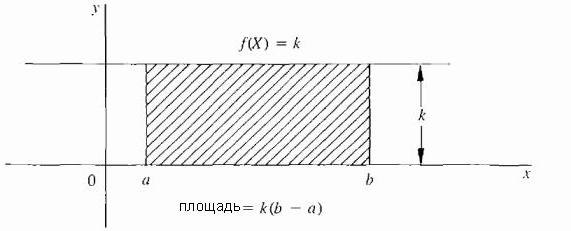 V tomto případě je plocha pod křivkou jen obdélník s výškou k a šířkou (b - a), takže oblast je definována jako: k · (b - a).
V tomto případě je plocha pod křivkou jen obdélník s výškou k a šířkou (b - a), takže oblast je definována jako: k · (b - a).
Oblasti některých dalších jednoduchých tvarů, jako je trojúhelník, lichoběžník a půlkruh, jsou dány planimetrickými vzorci.
Plocha pod jakoukoliv kontinuální křivkou y = f (x) je dána určitým integrálem, který je psán stejným způsobem jako normální integrál.
Riemannův součet
Než se ponoříme do detailní odpovědi na otázku, co je nedílnou součástí, zdůrazňujeme některé základní myšlenky.
Nejprve je plocha pod křivkou rozdělena na určitý počet n svislých pruhů s dostatečně malou šířkou Δx. Dále je každý vertikální proužek nahrazen svislým obdélníkem o výšce f (x), šířce Δx a oblasti f (x) dx. Dalším krokem je vytvoření součtu ploch všech těchto obdélníků nazývaných Riemannian sum (viz obrázky níže).
Vykreslením obdélníků Δx wide můžeme uvést jejich výšku rovnou hodnotě funkce na levém okraji každého pásu, tj. Křivka bude extrémně levý bod jejich horních krátkých stran Δx široký. Současně v části, kde funkce roste a její křivka je konvexní, jsou všechny obdélníky pod touto křivkou, tj. Jejich součet bude jistě nižší než přesná hodnota plochy pod křivkou v této oblasti (viz obrázek níže). Tato metoda přiblížení se nazývá levostranná. 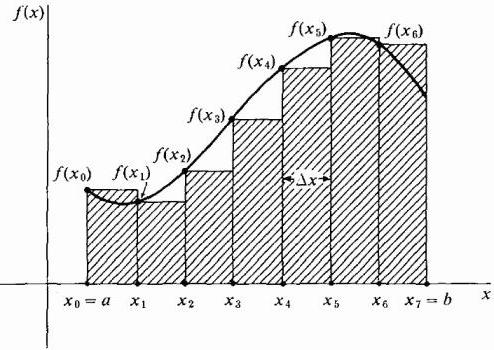
V zásadě lze nakreslit přibližné obdélníky takovým způsobem, že extrémně pravé body jejich horních krátkých stran šířky Δx leží na křivce. Pak budou vyšší než křivka a přiblížení plochy v této oblasti bude větší než její přesná hodnota, jak je znázorněno na obrázku níže. Tato metoda se nazývá správná. 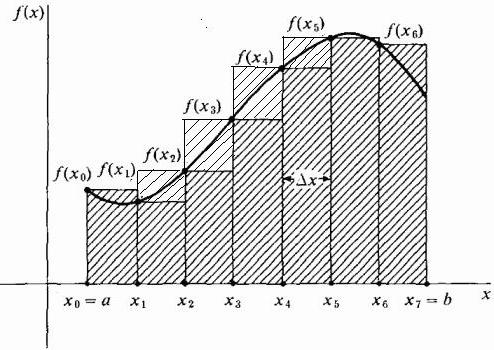
Ale můžeme také vzít výšku každého přibližného obdélníku rovnající se pouze nějaké hodnotě funkce v libovolném bodě x * i uvnitř odpovídajícího pásu Δx i (viz obr. níže). V takovém případě nemůžeme mít stejnou šířku všech pásů. 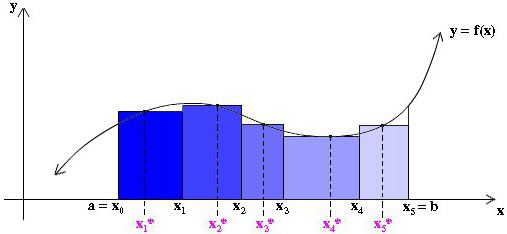
Riemannovou částku činíme:

Přechod z Riemannovy sumy na určitý integrál
Ve vyšší matematice je prokázána věta, která říká, že pokud neomezený nárůst počtu n přibližných obdélníků má jejich největší šířka tendenci k nule, pak Riemannian součet A n má tendenci k nějakému limitu A. Číslo A je stejné pro jakýkoli způsob tvorby přibližných obdélníků a pro libovolný výběr bodů x * i .
Jasné vysvětlení věty je uvedeno na následujícím obrázku.
Ukazuje, že čím užší obdélníky, tím bližší je oblast stupňovité postavy na plochu pod křivkou. Pokud je počet obdélníků n → ∞, jejich šířka je Δx i → 0 a limita A součtu A n je číselně rovna požadované oblasti. Tento limit a existuje určitý integrál funkce f (x): 
Integrální symbol, který je modifikovaným kurzívou S, byl představen Leibnizem. J. B. Fourier navrhl, aby notaci integrálu v horní a spodní části. Současně jsou jasně uvedeny počáteční a konečné hodnoty x.
Geometrická a mechanická interpretace určitého integrálu
Pokusíme se podrobně odpovědět na otázku, co je integrál? Zvažme integrál v intervalu [a, b] z kladné funkce f (x) uvnitř a předpokládáme, že horní hranice je větší než dolní a Pokud jsou souřadnice funkce f (x) v záporné hodnotě uvnitř [a, b], absolutní hodnota integrálu se rovná oblasti mezi osou x a grafem y = f (x), integrál sám o sobě je záporný. V případě jediného nebo opakovaného průsečíku osy y = f (x) na úsečce [a, b], jak je znázorněno na obrázku níže, pro výpočet integrálu je nutné určit rozdíl, ve kterém se pokles rovná celkové ploše plotů nad osou x a odpočitatelná - celková plocha ploch pod ním. Mechanická interpretace určitého integrálu úzce souvisí s geometrií. Vraťme se do sekce "Riemann sum" a představte si, že graf zobrazený na obrázcích vyjadřuje funkci rychlosti v = f (t) s nerovnoměrným pohybem materiální bod (osa úsečky je časová osa). Pak oblast libovolného aproximačního obdélníku o šířce Δt, kterou jsme vytvořili při tvorbě součtu Riemann, vyjádří přibližně dráhu bodu v čase Δt, konkrétně v (t *) Δt. Celkový součet ploch obdélníků na intervalu od t 1 = a do t 2 = b vyjadřuje přibližně cestu s během doby t 2 - t 1 a její mez, tj. integrál (definovaný) od a do b funkce v = f (t) přes dt udává přesnou hodnotu cesty s. Pokud se vrátíme k jeho označení, pak můžeme předpokládat, že a = const, a b je specifická hodnota nějaké nezávislé proměnné x. Pak určitý integrál s horní hranicí x z konkrétního čísla se změní na funkci x. Tento integrál se rovná oblasti obrázku pod křivkou uvedenou body aABb na obrázku níže. Předpokládejme, že jsme proměnné x = b nějaký malý přírůstek Δx. Pak se přírůstek plochy tvaru aABb skládá z plochy obdélníku (stínované na obrázku) Bb ∙ Δx a plochy obrázku BDC pod křivkou. Plocha obdélníku se rovná Bb ∙ Δx f = f (x) Δx, to znamená, že jde o lineární funkci přírůstku nezávislé proměnné. Oblasť tvaru BDC je zjevně menší než plocha obdélníku BDCK = Δx ∙ Δy a jako Δx → 0 má tendenci klesat ještě rychleji než je. Proto je f (x) Δx = f (x) dx rozdíl diferenciální oblasti aABb, tj. Diferenciál určitého integrálu Z toho můžeme konstatovat, že výpočet integrálů spočívá v nalezení funkcí z daných výrazů jejich diferenciálů. Integrální počet je přesně systém metod pro nalezení takových funkcí od jejich známých rozdílů. Spojuje vztah mezi diferenciací a integrací a ukazuje, že existuje operace inverzní k diferenciaci funkce - její integrace. Ukazuje také, že pokud je nějaká funkce f (x) spojitá, pak pomocí této matematické operace najde celý soubor (set, set) funkcí primitivních pro ni (nebo jinak, najděte z neho neurčitý integrál). Nechť funkce F (x) je označení výsledku integrace funkce f (x). Korespondence mezi těmito dvěma funkcemi v důsledku integrace druhé z nich je uvedena následovně: Jak je vidět, s integrálním symbolem nejsou žádné integrační limity. To znamená, že od určitého je transformován do neurčitého integrálu. Slovo "neurčité" znamená, že výsledek integrační operace v tomto případě není jeden, ale mnoho funkcí. Ve skutečnosti, kromě funkce F (x), jakákoli funkce F (x) + C splňuje poslední výrazy, kde C = const. Z toho vyplývá, že stálý člen v sestavě antiderivátů může být nastaven libovolně. Je třeba zdůraznit, že jestliže integrál definovaný funkcí je číslo, pak neurčitý je funkce, přesněji jejich sada. Termín "integrace" se používá k definování vyhledávání obou typů integrálů. Je to úplný opak odpovídajícího pravidla pro diferenciaci. Jak jsou odebírány neurčité integrály? Příklady tohoto postupu považujeme za specifické funkce. Podívejme se na výkonovou funkci obecné podoby: f (x) = cx n Poté, co jsme to udělali s každým výrazem ve výrazu integrovatelné funkce (pokud existuje několik), přidáme konstantu na konci. Připomeňme, že odvození derivátu s konstantní hodnotou ji ničí, takže převzetí integrálu nějaké funkce nám poskytne obnovu této konstanty. Označujeme to C, protože konstanta je neznámá - může to být libovolné číslo! Proto můžeme mít nekonečně mnoho výrazů pro neurčitý integrál. Podívejme se na jednoduché neurčité integrály, jejichž příklady jsou uvedeny níže. Předpokládejme, že musíte najít integrální funkci: f (x) = 4 x 2 + 2x - 3. Začneme s prvním semestrem. Podíváme se na exponent 2 a zvyšujeme jej o 1, pak rozdělíme první termín o výsledný ukazatel 3. Získáme: 4 (x 3 ) / 3. Pak se podíváme na dalšího člena a děláme totéž. Vzhledem k tomu, že má exponent 1, výsledný ukazatel bude 2. Tímto termínem rozdělíme 2: 2 (x 2 ) / 2 = x 2 . Poslední termín má faktor x, ale prostě to nevidíme. Poslední termín si můžeme představit jako (-3x 0 ). To odpovídá (-3) ∙ (1). Použijeme-li integrační pravidlo, přidáme 1 k ukazateli, abychom jej zvýšili na první stupeň, a pak rozdělíme poslední termín o 1. Získáme 3x. Toto integrační pravidlo funguje pro všechny hodnoty n, s výjimkou n = - 1 (protože se nedá rozdělit o 0). Považovali jsme za nejjednodušší příklad nalezení integrálu. Obecně řečeno, řešení integrálů není snadným úkolem a zkušenosti, které již získal v matematice, jsou v něm dobrou pomocí. V části výše jsme zjistili, že z každého vzorce diferenciace je získán odpovídající integrační vzorec. Proto jsou všechny jejich možné možnosti již dlouho získány a shrnuty v odpovídajících tabulkách. Následující tabulka integrálů obsahuje vzorce pro integraci základních algebraických funkcí. Tyto vzorce je třeba vzpomenout a postupně je zapamatovat, protože jsou to fixní cvičení. Další tabulka integrálů obsahuje hlavní trigonometrické funkce: Ukazuje se, že k tomu, aby bylo možné integrovat, to znamená najít neurčité integrály, je velmi jednoduché. A na tom pomáhá vzorec zakladatelů integro-diferenciálního kalkulu Newton-Leibniz. Podle toho v první fázi výpočet požadovaného integrálu spočívá ve zjištění neurčitosti a potom výpočtu hodnoty nalezeného primitivního F (x) se substitucí x, rovnající se nejdříve horní hranici, potom nižší a nakonec určení rozdílu těchto hodnot. V tomto případě nelze konstantu C zapsat. protože zmizí při odčítání. Některé integrály považujeme za detailní řešení. Najděte oblast pod jednou polovinou vlnové sínusové vlny. Nyní považujeme integrály s detailním řešením, které využívá vlastnost aditivity v prvním příkladu, a nahrazení mezilehlé integrační proměnné ve druhém příkladu. Vypočítáme určitý integrál frakční racionální funkce: y = (1 + t) / t 3 od t = 1 do t = 2. Nyní ukážeme, jak zjednodušit uchopení integrálu zavedením mezilehlé proměnné. Předpokládejme, že musíte vypočítat integrál (x + 1) 2 . Mluvili jsme o určitém integrálu pro konečný interval [a, b] funkce f (x) kontinuální na něm. Ale řada specifických problémů vede k potřebě rozšířit koncepci integrálu o případ, kdy se limity (jedna nebo obě) rovnají nekonečnu, nebo pokud je diskontinuální funkce. Například při výpočtu ploch pod křivkami, které se asymptoticky přibližují osám souřadnic. Pro rozšíření konceptu integrálu na tento případ se kromě průchodu k hranici při výpočtu součtu Riemann přibližných obdélníků provede další. S takovým dvojitým průchodem do hranice se získá nesprávný integrál. Naproti tomu všechny výše uvedené integrály se nazývají správné. 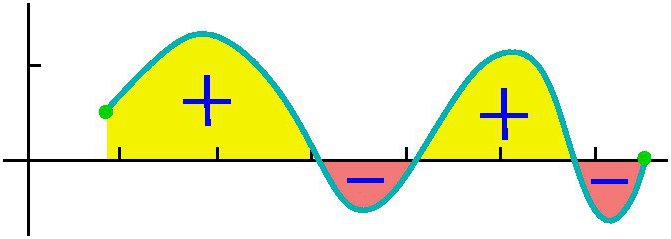 Takže pro funkci zobrazenou na obrázku výše, určitý integrál od a do b bude (S1 + S3) - (S2 + S4).
Takže pro funkci zobrazenou na obrázku výše, určitý integrál od a do b bude (S1 + S3) - (S2 + S4). Diferenciál určitého integrálu
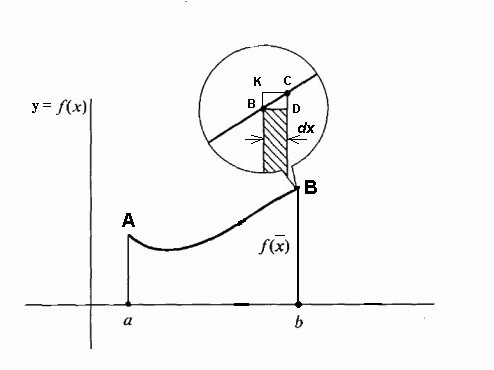 S pevnou linií aA a pohyblivou Bb se tato oblast stává funkcí f (x), přičemž přírůstky Δx jsou stále uloženy podél osy x a přírůstky funkce f (x) jsou přírůstky plochy pod křivkou.
S pevnou linií aA a pohyblivou Bb se tato oblast stává funkcí f (x), přičemž přírůstky Δx jsou stále uloženy podél osy x a přírůstky funkce f (x) jsou přírůstky plochy pod křivkou. 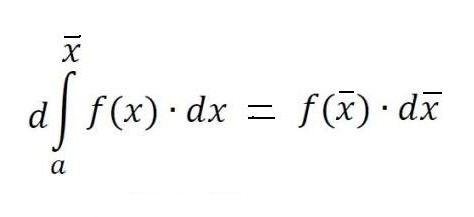
Základní poměr integrálního počtu
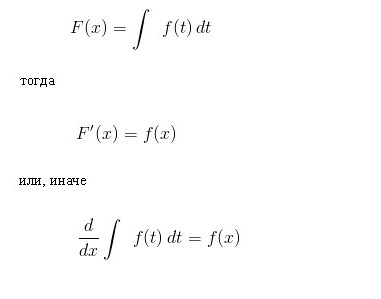
Základní pravidlo integrace

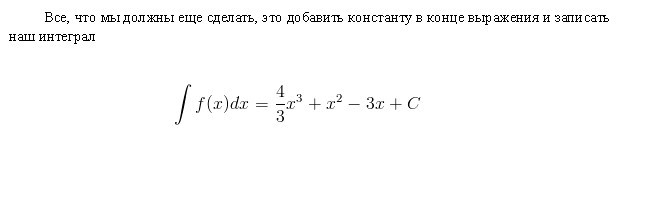

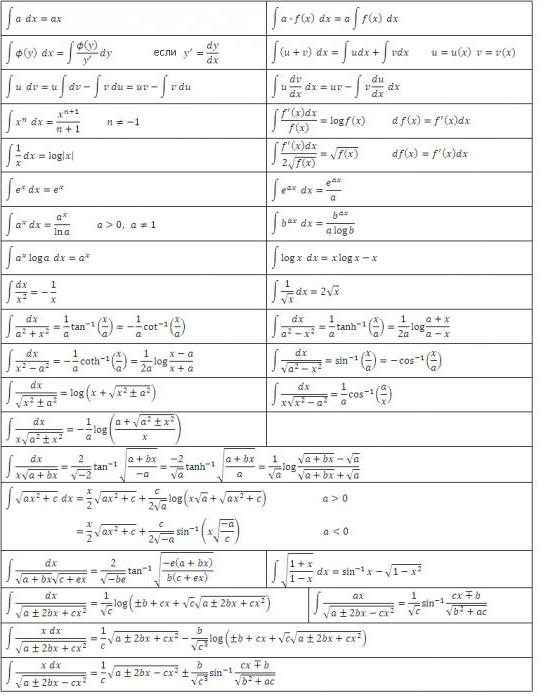
Integrální tabulky

Jak vypočítat určitý integrál
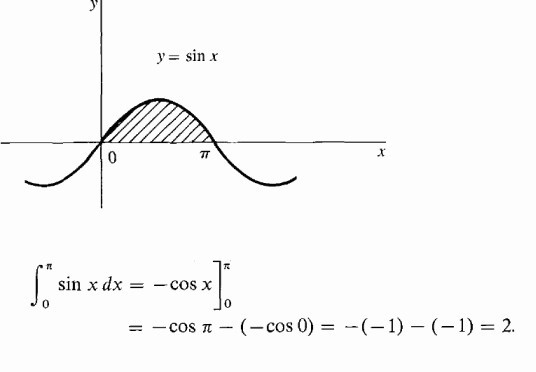 Vypočítejte stínovanou oblast pod nadsázkou.
Vypočítejte stínovanou oblast pod nadsázkou. 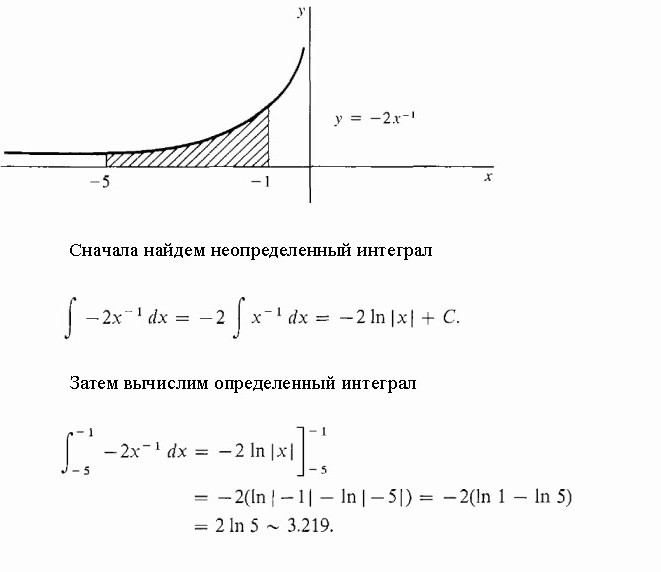
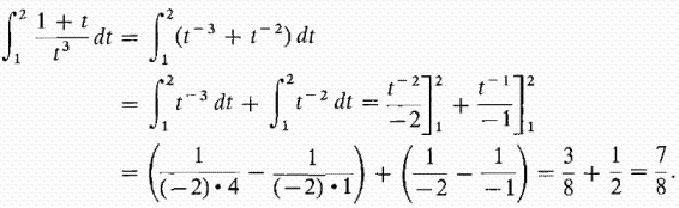
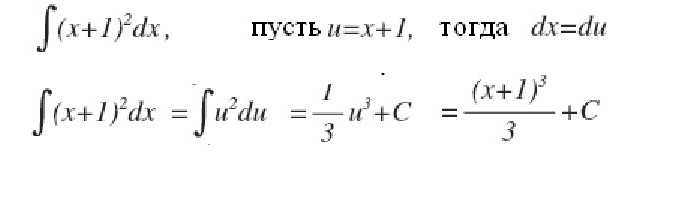
O nevhodných integrálech