Jak najít oblast polygonu?

Při problémech s geometrií je často nutné vypočítat plochu polygonu. Navíc může mít trochu různorodý tvar - od známého trojúhelníku až po určitého n-gona s nepředstavitelným počtem vrcholů. Tyto polygony jsou navíc konvexní nebo konkávní. V každé situaci se předpokládá, že staví na vzhledu postavy. Zdá se tedy, že zvolíte nejlepší způsob řešení problému. Tvar může být správný, což výrazně zjednoduší řešení problému.

Trochu teorie polygonů

Pokud jsou kresleny tři nebo více protínajících přímky, tvoří určitou postavu. To je polygon. Podle počtu průsečíků je jasné, kolik vrcholů bude mít. Dávají název výsledného čísla. Může to být:

• trojúhelník;
• čtyřúhelník;
• penta nebo hexagon a tak dále.

Taková čísla budou jistě charakterizována dvěma ustanoveními:

1. Sousední strany nepatří k jedné přímce.
2. Nesousedící body nemají společné body, to znamená, že se neprotínají.

Chcete-li zjistit, které vrcholy jsou přilehlé, musíte zjistit, zda patří ke stejné straně. Pokud ano, další. V opačném případě mohou být spojeny segmentem, který musí být označen jako úhlopříčka. Mohou být nakresleny pouze v polygonech, které mají více než tři vrcholy.

Jaké jsou jejich typy?

Víceúhelník s více než čtyřmi rohy může být konvexní nebo konkávní. Rozdíl je v tom, že některé jeho vrcholy mohou ležet na protilehlých stranách přímky vedené libovolnou stranou polygonu. V konvexním případě jsou všechny vrcholy vždy na jedné straně takové linie.

V průběhu geometrie školy se většinou věnuje přesně konvexním číslům. Proto je v problémech nutné zjistit plochu konvexního mnohoúhelníku. Potom je k dispozici vzorec přes poloměr ohraničeného kruhu, který vám umožní najít požadovanou hodnotu pro libovolný tvar. V jiných případech neexistuje jedinečné řešení. Pro trojúhelník je vzorec jeden a pro čtverec nebo lichoběžník úplně jiný. V situacích, kdy je tvar nepravidelný nebo je spousta vrcholů, je obvyklé, že je rozdělíme na jednoduché a známé.

Co dělat, když kus má tři nebo čtyři vrcholy?

V prvním případě to bude trojúhelník a můžete použít jednu z následujících vzorců:

• S = 1/2 * a * n, kde a je bok, n je jeho výška;
• S = 1/2 * a * b * sin (A), kde a a b jsou strany trojúhelníku, A je úhel mezi známými stranami;
• S = √ (p * (p - a)) (p - c) * (p - c)), kde c je strana trojúhelníku, již označené dva, p je semiperimetr, .

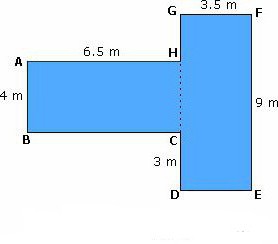
Obrázek se čtyřmi vrcholy může být rovnoběžníkem:

• S = a * n;
• S = 1/2 * d ₁ * d ₂ * sin (α), kde d ₁ a d ₂ jsou diagonály, α je úhel mezi nimi;
• S = a * v * sin (α).

Vzorec pro trapézní oblasti: S = n * (a + b) / 2, kde a a b jsou délky základů.

Co dělat s pravidelným polygonem s více než čtyřmi vrcholy?

Na začátku je taková postava charakterizována skutečností, že v ní jsou všechny strany stejné. Navíc má mnohoúhelník stejné úhly.

Je-li kolem takovéto postavy popsána kružnice, pak její poloměr se shoduje se segmentem od středu polygonu k jednomu z vrcholů. Proto pro výpočet plochy pravidelného polygonu s libovolným počtem vrcholů potřebujeme následující vzorec:

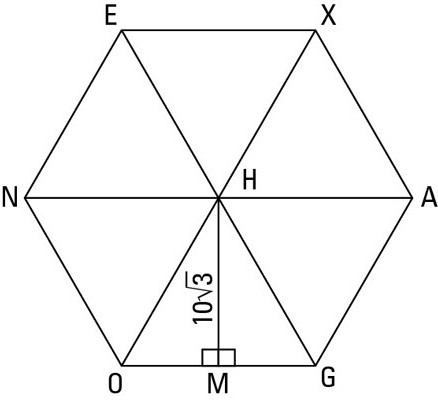
S _n = 1/2 * n * R _n ² * sin (360 ° / n), kde n je počet vrcholů polygonu.

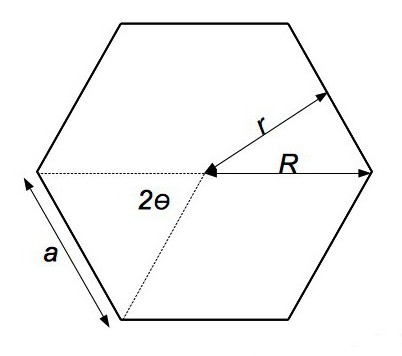
Z toho je snadné získat jeden, který je vhodný pro zvláštní případy:

1. trojúhelníky: S = (3√3) / 4 * R2;
2. čtverec: S = 2 * R2;
3. hexagon: S = (3√3) / 2 * R2.

Situace se špatným číslem

Cesta pro zjištění oblasti polygonu, pokud není správná a nemůže být přičítána žádnému z dříve známých čísel, je algoritmus:

• rozdělit je do jednoduchých tvarů, jako jsou například trojúhelníky, aby se neprotínají;
• vypočítat jejich plochu pomocí libovolného vzorce;
• doplňte všechny výsledky.

Co dělat, pokud jsou v daném problému uvedeny souřadnice vrcholů polygonu?

To znamená, že je známa sada dvojic čísel pro každý bod, která omezují strany postavy. Obvykle jsou psány jako (x ₁ ; y ₁ ) pro první, (x ₂ ; y ₂ ) pro druhý a nth vrchol má tyto hodnoty (x _n ; y _n ). Pak je oblast polygonu definována jako součet n pojmů. Každý z nich vypadá takto: ((y _{i + 1} + y _i ) / 2) * (x _{i + 1} - x _i ). V tomto výrazu se liší od jednoho do n.

Je třeba poznamenat, že označení výsledku bude záviset na obejití tvaru. Při použití specifikovaného vzorce a pohybu ve směru hodinových ručiček bude odpověď záporná.

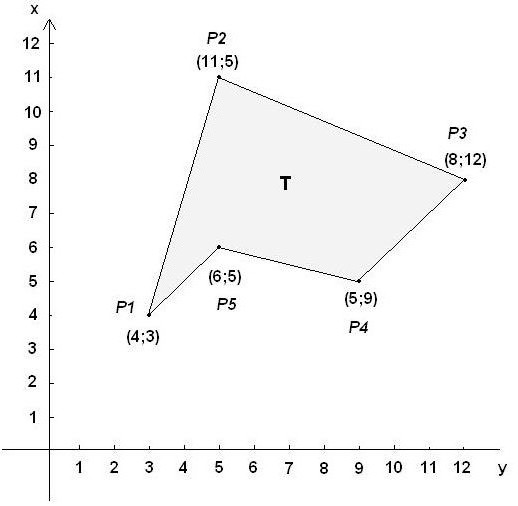
Příklady úkolů

Stav Souřadnice vrcholů jsou dány hodnotami (0.6; 2.1); (1.8; 3.6); (2.2; 2.3); (3.6; 2.4); (3.1; 0.5). Požadováno pro výpočet plochy polygonu.

Rozhodnutí. Podle výše uvedeného vzorce bude první termín (1,8 + 0,6) / 2 * (3,6 - 2,1). Zde stačí vzít hodnoty pro hru a X od druhého a prvního bodu. Jednoduchý výpočet vede k výsledku 1,8.

Druhý termín je podobně získán: (2.2 + 1.8) / 2 * (2.3 - 3.6) = -2.6. Při řešení těchto problémů se nebojte negativních hodnot. Všechno je v pořádku. To je plánováno.

Podobně jsou získány hodnoty pro třetí (0,29), čtvrtou (-6,365) a pátou (2,96). Celková plocha je tedy 1,8 + (-2,6) + 0,29 + (-6,365) + 2,96 = - 3,915.

Rada pro řešení problému, pro který je polygon zobrazen na papíře v buňce

Nejčastěji je záhadou, že v datových údajích existuje pouze velikost buněk. Ukázalo se však, že není zapotřebí více informací. Doporučení k vyřešení tohoto problému je rozdělení tvaru na mnoho trojúhelníků a obdélníků. Jejich prostor je poměrně snadné počítat délku stran, které se pak snadno skládají.

Ale často existuje jednodušší přístup. Spočívá v kreslení čísla do obdélníku a výpočtu hodnoty jeho plochy. Poté počítat oblasti těch prvků, které byly nadbytečné. Odčtěte je od celkového počtu. Tato možnost někdy zahrnuje mírně menší počet akcí.