Jaký je princip farmy?
XVII století bylo poznamenáno rychlým vývojem v Evropě zvláštního úseku fyziky - optiky. Zákony reflexe a refrakce byly otevřené světlu a Fermatův princip ukázal, proč mají odpovídající matematickou podobu. Podívejme se podrobněji na to, jaká je tato zásada.
Refrakční a reflexní jevy

Reflexí rozumí fenoménu, ve kterém světlo, šířící se v látce, která je pro něj transparentní, narazí na překážku v jeho cestě a drasticky mění jeho trajektorii. Každá překážka může být jakákoliv: tekutá nebo pevná, průhledná a neprůhledná.
Fenomén reflexe byl znám již od starověku. Podle historických důkazů byly zákony reflexe formulovány již před naší dobou. A v prvním století nl egyptský filozof Heron z Alexandrie vyjádřil myšlenku trajektorie světla, kterou francouzský Pierre Fermat později použil při formulaci svého principu.

Fenomén lomu je zlomenina přímky, podél které se světlo pohybuje, když překročí povrch oddělující dva průhledné materiály. Všimněte si, že v případě odrazu se paprsek pohybuje v jednom průhledném materiálu nebo, jak se říká, na jednom médiu.
První formulace zákonů lomu je přičítána perským matematikům 10. století k jistému Ibnu Sahlovi, který se ve svých dílech spoléhal na díla Claudia Ptolemaia (1. - 2. století). Na přelomu konce XVI. - začátku XVII. Století, holandský vědec Snell, shrnující výsledky mnoha experimentů se světlem, formuloval v matematické formě druhý zákon refrakce, který nyní nese jeho příjmení. Snell dal své znění z hlediska vzdáleností, nikoli úhlů, jak je obvyklé. Moderní vzhled zákona lomu již dal René Descartes.
Zákony šíření světla v průhledných médiích
Než začneme zvažovat princip Fermat, měly by být formulovány zákony refrakce a reflexe světla. Pro každý z těchto jevů je obvyklé vyčíst dva zákony. Níže jsou kombinovány ve dvojicích:
- Trajektorie nosníku, když překračuje rozhraní mezi dvěma médii, vždy leží ve stejné rovině jako normální rovina této hranice. Možná dráha paprsku je tvořena v obecném případě ze tří částí: dopadající paprsek, lomený a odražený.
- Pokud se úhel mezi dopadajícím světelným paprskem a normálem nazývá θ 1 , stejný úhel, ale pro odražený paprsek, je zapsán jako θ 2 a lom přemostění je θ 3 , pak 2. zákon bude vypadat takto:
- pro odraz: θ 1 = θ 2 ;
- pro refrakce: n 1 * sin (θ 1 ) = n 2 * sin (θ 3 ).
V těchto vzorcích jsou n 1 a n 2 indexy lomu v průhledných médiích 1 a 2. Index lomu se podle definice vypočítává takto:
n = c / v.
Zde v a c jsou rychlosti pohybu světelného paprsku v médiu a ve vakuu.
Formulace principu farmy

Pierre Fermat byl jedním z proslulých matematiků a právníků Francie v první polovině sedmnáctého století. Princip, který nese jeho jméno, formuloval v roce 1662, tedy půl století poté, co Snell objevil svůj zákon pro lámání.
Stručně, princip Fermat může být formulován následovně: světlo, když se pohybuje v absolutně průhledném médiu, vybírá takovou trajektorii, kterou prochází v co nejkratším čase.
Ve skutečnosti se tato formulace nijak neliší od toho, kterou Heron z Alexandrie udělal o půl tisíce let dříve pro fenomén reflexe. Francouz se však stal společným všem jevům spojeným se světlem a ukázal, jak mohou být z tohoto principu odvozeny zákony refrakce a reflexe.
Závěr prvního zákona reflexe
Pomocí principu Fermat budou matematické pojmy reflexe získány. Chcete-li to provést, zvažte níže uvedený obrázek.
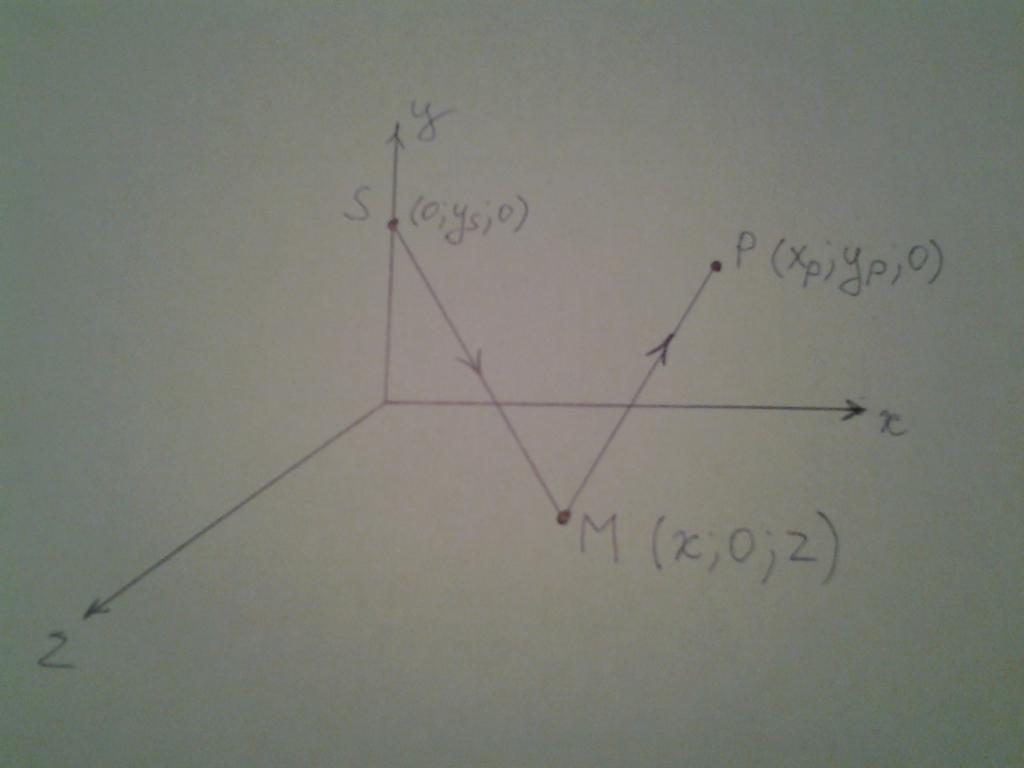
Zde je ukázáno, že paprsek vystupuje z bodu S, který leží na ose y. Pak se odráží od roviny xz v neznámém bodě M. Po odrazu se paprsek přesune do bodu P ležícího na rovině xy. Vybraná pozice bodů S a P nemá vliv na obecnost dalšího odůvodnění, ale pouze zjednodušuje matematické výpočty.
Takže zapisujeme souřadnice každého bodu:
S (0; yS; 0);
M (x; 0, z);
P (x P ; y P ; 0).
Souřadnice polohy bodů S a P jsou známy. Úkolem je najít takový bod M, který bude odpovídat skutečné dráze SMP procházející světelným paprskem. Předpokládáme také, že uvažovaný prostor je homogenní, to znamená, že rychlost světla v kterémkoli okamžiku je konstantní hodnotou.
Podle principu Fermat, trajektorie SMP světla projde v co nejkratší době, pokud je to co nejkratší. Napíšeme jeho délku:
SM = √ (x 2 + y S 2 + z 2 ); MP = √ ((xx P ) 2 + y P 2 + z 2 );
SMP = √ (x 2 + y S 2 + z 2 ) + √ ((xx P ) 2 + y P 2 + z 2 ).
Pro výpočet minimální délky SMP je nutné najít částečné deriváty s ohledem na x a z (neznámé souřadnice bodu M) a rovnat získané výsledky na nulu.
Nejprve nalezneme částečný derivát s ohledem na z. Máme:
∂ (SMP) / ∂z = z / √ (x 2 + y S 2 + z 2 ) + z / √ ((xx P ) 2 + y P 2 + z 2 ) = 0.
Tato rovnost má jediný kořen při z = 0. Jinými slovy, bod M leží na ose x, tj. Ve stejné rovině jako body P a S (rovina xy). Z toho vyplývá, že obnovená normálová rovina xz, ve které se podle stavu problému nachází bod M, bude mít SM a MP ve stejné rovině (xy). Toto je první zákon reflexe.
Závěr druhého zákona reflexe
Pokračujte ve výpočtu předchozí položky. Jak bylo řečeno, je nyní nutné najít částečný derivát s ohledem na x. Máme:
∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ =
Napsali jsme poslední rovnost ve formě:
x / SM + (xx P ) / MP = 0 =>
x / SM = (x P- x) / MP.
Vztahy získané v každé části rovnosti jsou úhly úhlů s vrcholem v bodech S a P. Pokud nyní obnovíme normální rovinu xz přes bod M, pak označené úhly budou odpovídat úhlu dopadu (mezi SM a normálu) a odrazům (mezi MP a normálem) .
Takže podle principu Fermat jsme získali i druhý zákon odrazu světla.
Závěr zákona lomu Snell
Nyní ukážeme, jak lze zákon o refrakci světla odvodit z principu Fermat. Chcete-li to provést, zvažte podobný obrázek jako předchozí.
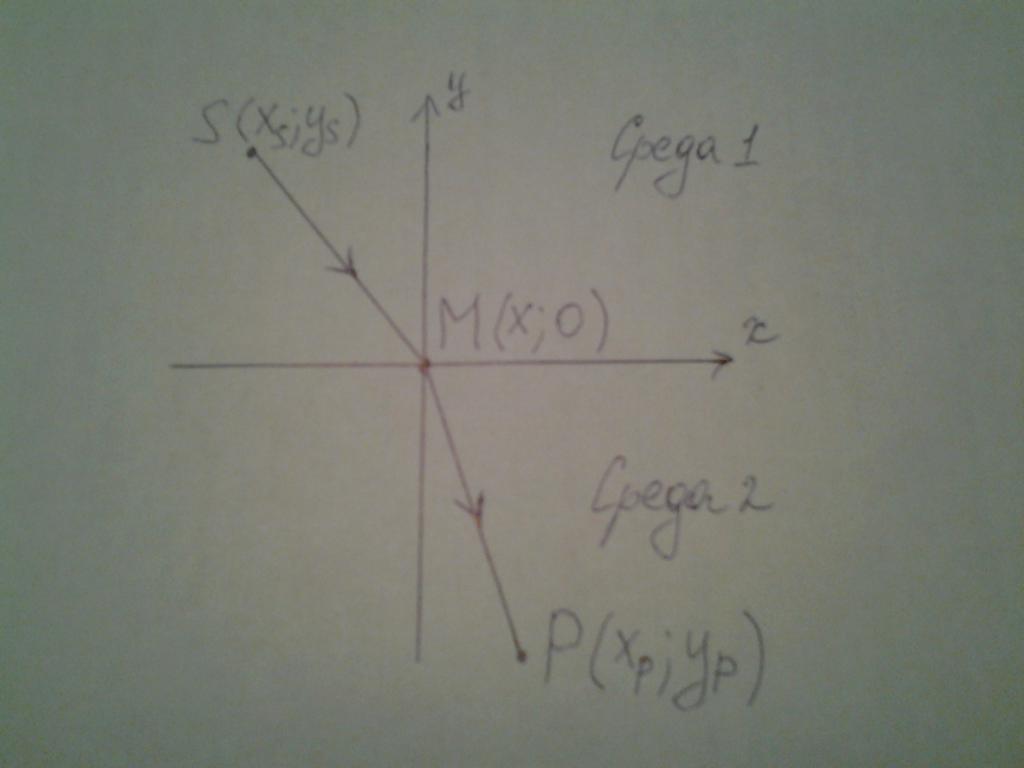
Pro jednoduchost budeme zvažovat případ v rovině xy. Zapisujeme souřadnice zdroje S a světla přijímače P, které jsou v různých prostředích:
S ( xS ; yS);
M (x; 0);
P (x P ; y P ).
Najdeme neznámou souřadnici bodu M. Koordinace y = 0 je přesně známá, protože právě na hranici média (osa x) se změní rychlost světla. Délky segmentů SM a MP se rovnají:
SM = √ (xx S ) 2 + y S 2 );
MP = √ (x P- x) 2 + y P 2 ).
Celkový čas, který světlo vynaloží na trasu SMP, se bude rovnat:
t = SM / v 1 + MP / v 2 .
Zde v1 a v2 jsou rychlosti paprsku v odpovídajícím médiu. Abychom zjistili minimální dobu pohybu, měli bychom vzít celkový derivát s ohledem na proměnnou x a rovnat jej na nulu. Máme:
dt / dx = (xx S ) / (√ (xx S ) 2 + yS 2 ) * v 1 ) - (x P -x) / (√ (x P -x) 2 + y P 2 ) ) = 0 =>
(xxS) / (SM * v1) = (xP-x) / (MP * v 2 ).
Pomocí funkcí sinus úhlu dopadu θ 1 a lomu θ 3 získáváme:
sin (θ 1 ) / v 1 = sin (θ 3 ) / v 2 .
Abychom dosáhli získané rovnosti Snellově zákonu v pohodlné podobě (prostřednictvím indexů lomu médií), je nutné vynásobit levé a pravé strany rychlostí světla c.

Použití principu Fermat umožňuje snadné vyvozování zákonů o hlavních jevech pohybu světelného paprsku v průhledných materiálech.
Pohyb světla v nehomogenním prostředí
Uvedené případy předpokládají, že materiál je homogenní a světelný paprsek si zachovává svou rychlost při pohybu. V případě nehomogenních médií platí následující rovnost:
L = ∫n (x, y, z) * dl.
Tento integrál je veden podél světelné trajektorie. Diferenciál dl je segment cesty, pro kterou médium zachovává svou homogenitu. Hodnota n (x, y, z) je lokální index lomu.
Označený integrál se obvykle nazývá integrál optické dráhy. Princip farmy pro optickou cestu zahrnuje nalezení extrémů pro L.
Obecná formulace uváděného principu
Princip minimálního času pro pohyb světla je specifický pro obecnější formulaci. V současné době je obecný princip Fermat formulován takto: Světlo zvolí trajektorii během pohybu, která odpovídá extrémům optické dráhy.
Extrémy funkce podle matematické definice jsou minimální, maximální a inflexní bod. Obecný princip Fermatu vyhovuje všem těmto hodnotám, to znamená, že trajektorie světla nemusí být nutně minimální, může to být jak maximální, tak odpovídající inflexní bod optické dráhy.
Domácí analogie s uvažovaným principem
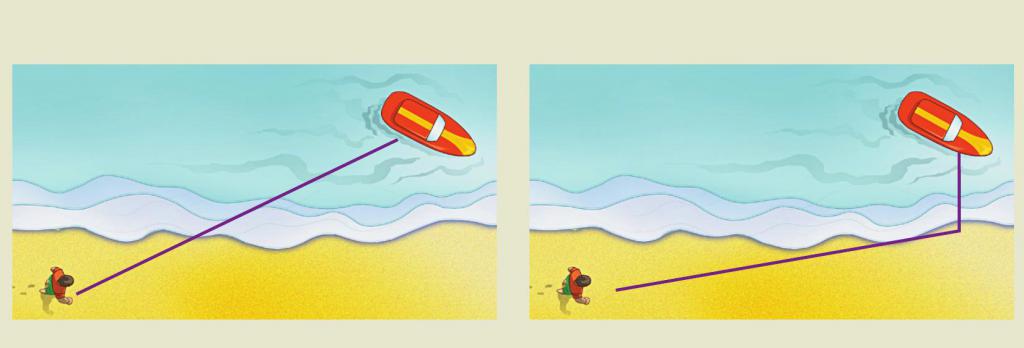
Obecná zásada Fermatu je naopak zvláštní případ takzvaného principu nejmenšího jednání. Zde neposkytneme odpovídající definice a jejich matematické formulace, nicméně ukážeme, kde lze uplatnit zásadu navrženou Francouzi.
Používá se při řešení jednoduchého, na první pohled každodenní úkol: například se člověk utopí v moři poblíž pláže. Jak by se měl záchranář pohybovat na břehu, aby zachránil utopeného? Samozřejmě, že by se měl dostat na záchranu v nejmenším čase. Vzhledem k tomu, že rychlost pohybu plavčíka na pláži je více než na vodě, měl by běžet nějakou vzdálenost podél břehu, a teprve pak skákat do vody a plavat. To znamená, že úkol je omezen na uplatnění principu Fermat, kde role světelného paprsku hraje záchranář.
Všimněte si, že řešení tohoto problému není jednoduché, protože ve svém procesu se objevují rovnice 4. stupně.
Princip Fermat je tedy nástrojem pro získání základních zákonů šíření světla. Nicméně to není zásadní. Lze říci, že z Huygensova principu zdrojů sekundárních sférických vln vyplývá.